Matematické Kalkulačky
Kalkulačka Pravděpodobnosti
Kalkulačka pravděpodobnosti vám umožní prozkoumat vztahy pravděpodobnosti mezi dvěma samostatnými událostmi. To vám umožní lépe porozumět tomu, jak spolu události souvisí, a díky tomu jsou předpovědi přesnější.
Pravděpodobnosti jednotlivých událostí
%
%
Jakou pravděpodobnost chcete vidět?
%
Pravděpodobnosti řady událostí
časy
%
Obsah
| ◦Definice pravděpodobnosti |
| ◦Podmíněná pravděpodobnost |
| ◦Teoretická vs experimentální pravděpodobnost |
| ◦Pravděpodobnost a statistika |
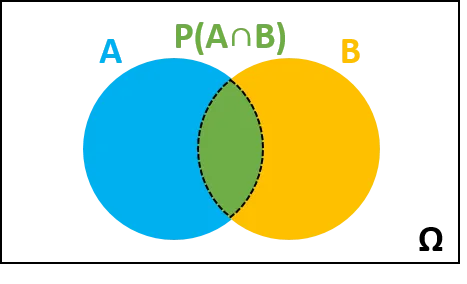
Kalkulačka pravděpodobnosti je užitečným nástrojem při zkoumání vztahů mezi událostmi, jako je pravděpodobnost, že se stane A a pravděpodobnost, že se stane B. Je-li například pravděpodobnost, že se stane A, 50 % a stejná pro B, jaká je pravděpodobnost, že se stane obojí, stane se pouze jeden, alespoň jeden, nebo se nestane ani jedno, a tak dále?
Naše pravděpodobnostní kalkulačka vám pomůže vidět pravděpodobnost šesti různých scénářů. Navíc, když zadáte, kolikrát je kostka vržena, získáte další čtyři scénáře. Tímto způsobem nemusíte provádět všechny výpočty sami. Stačí zadat čísla a naše kalkulačka se postará o zbytek!
Definice pravděpodobnosti
Pravděpodobnost je způsob uvažování o nejistých situacích a používá se v různých oblastech, jako je hazard, rozhodování a statistika. Definice pravděpodobnosti uvedená v tomto kurzu je nejzákladnější a nejzákladnější definicí předmětu.
Podmíněná pravděpodobnost
Pravděpodobnost je především o studiu náhody a jedním z nejdůležitějších konceptů, kterým je třeba porozumět, je, zda jsou události závislé nebo ne. Dvě události jsou nezávislé, pokud výskyt první neovlivňuje pravděpodobnost výskytu druhé. To je neuvěřitelně důležité, protože to určuje, jak můžeme vypočítat potenciální výsledky. Pokud hodíme dokonale vyváženou standardní krychlovou kostkou, je 1/6 šance, že dostaneme dvojku.
I když byly kostky v tomto příkladu spojeny dohromady, pravděpodobnost získání dvojky ⚁ ve druhém tahu je stále 1/6, protože události jsou nezávislé. To znamená, že pravděpodobnost získání alespoň jednoho konkrétního výsledku, například dvojky ⚁ v prvním tahu, nezávisí na tom, co se stane s kostkami ve druhém tahu.
Pravděpodobně existují různé způsoby pohledu na scénář. Tentokrát budeme mluvit o podmíněné pravděpodobnosti. Předpokládejme, že hrajete tenis a jeden z vašich soupeřů se přiblíží k síti. V závislosti na úhlu, pod kterým zasáhli míč, může být možné poslat míč za soupeře jedním úderem. Pokud však jejich soupeř uhne, když uvidí přicházet míč, míč se pravděpodobně odrazí od země a jeho soupeř ho může chytit. Toto je příklad situace, kdy se o hře uvažuje z hlediska událostí (odpálení míče) a výsledků.
Teoretická vs experimentální pravděpodobnost
Ve většině případů je teoretická pravděpodobnost definována jako poměr mezi počtem příznivých výsledků a počtem všech možných výsledků. Existuje však rozdíl mezi teoretickou pravděpodobností a experimentální pravděpodobností. Formální definice experimentální pravděpodobnosti je poměr mezi počtem výsledků, které spadají do konkrétní kategorie (experimentu), k celkovému počtu výsledků. Experimentální design se opírá o dané informace, logické uvažování a říká nám, co můžeme od experimentu očekávat. V ideálním případě budou tyto informace pocházet z testované hypotézy. Po shromáždění těchto informací vám experimentální design pomůže navrhnout experiment způsobem, který potvrdí nebo zneplatní vaši hypotézu.
Ve hře 42 kuliček se náhodně vybere jedna kulička a nekonečněkrát se vrátí zpět do sáčku. To znamená, že v sáčku je vždy 42 kuliček, z toho 18 oranžových. Pravděpodobnost výběru konkrétní barvy můžeme vypočítat vydělením počtu kuliček této barvy celkovým počtem kuliček v sáčku (42). To je zjednodušeno na 3/7 nebo pravděpodobnost je 18/42, což znamená, že z každých 14 vybraných koulí by měly být 3 oranžové koule.
Pravděpodobnost je matematická věda, která se zabývá možností, že se něco stane. Lze jej použít k předpovědi toho, co se stane v důsledku provedení experimentu, nebo k pochopení pravděpodobnosti, že se v dané situaci něco stane. V tomto příkladu použijeme experimentální pravděpodobnost, abychom pochopili, co se stalo, když jsme vybrali kuličku z pytle a opakovali postup ještě 13krát. Předpokládejme, že jsme získali 8 oranžových míčků ve 14 pokusech. To nám dává empirickou pravděpodobnost 8 ze 14, neboli 44 %.
Budou chvíle, kdy si vyberete více karet, chvíle, kdy jich dostanete méně, a chvíle, kdy si vyberete předpokládaný počet. Výsledek se však bude od teoretického lišit. To se děje proto, že když se snažíte tuto hru opakovat znovu a znovu, někdy si vyberete více, někdy méně a někdy si vyberete přesně teoreticky předpokládané číslo. Pokud sečtete všechny výsledky, měli byste si všimnout, že celková pravděpodobnost se stále více blíží teoretické pravděpodobnosti. Pokud ne, pak může existovat rozpor mezi tím, co vidíte, a hypotetickým výsledkem – to může být například případ, kdy některé míčky v sáčku mají různé barvy a velikosti. Abyste získali přesný odhad, budete muset náhodně vybrat proces výběru.
Pravděpodobnost a statistika
Statistika je odvětví matematiky, které se zabývá sběrem, interpretací, analýzou, prezentací a interpretací dat. Pravděpodobnost je odvětví matematiky, které studuje možnost událostí a jejich výsledky. Je důležité těmto rozdílům porozumět, protože mohou v různých situacích vést k různým závěrům.
Pravděpodobnost je teoretická oblast matematiky, která se zabývá věcmi, jako jsou matematické definice a věty. Naproti tomu statistika je praktickou aplikací matematiky, která se snaží přisoudit smysl a porozumění pozorování v reálném světě. Statistiku lze rozdělit do dvou hlavních větví – deskriptivní a inferenční. Popisná statistika zkoumá popisné vlastnosti populace, jako jsou počty, průměry a standardní odchylky. Inferenční statistika používá statistické metody k vyvozování závěrů o populaci ze vzorků, buď z experimentu, nebo z pozorování převzatých z reálného světa.
Pravděpodobnost je schopnost předpovídat možnost událostí, zatímco statistika je studium frekvence minulých událostí. Na konci kurzu budete hlouběji rozumět těmto pojmům a budete schopni je použít k modelování reálných dat.
Předpokládejme, že hrajete hazardní hru, kde je každá karta vybrána se stejnou pravděpodobností a vaším cílem je vyhrát. V tomto případě byste mohli vsadit na základě kurzu – tedy pravděpodobnosti, že vámi vybraná karta bude piková. Za předpokladu, že balíček je kompletní a výběr je zcela náhodný a spravedlivý, můžete odvodit, že pravděpodobnost je rovna ¼. To znamená, že můžete s jistotou vsadit.
Statistik bude chvíli sledovat hru, aby posoudil férovost, než se poradí s pravděpodobnostním poradcem, jaké kroky podniknout, abyste měli největší šanci na výhru. Poté, co se dohodnou, že hrát hru stojí za to, pravděpodobnostní poradí, jaké kroky podniknout, aby zvýšili své šance.
Autor článku
John Cruz
John je doktorand s vášní pro matematiku a vzdělávání. Ve svém volném čase se John rád věnuje pěší turistice a jízdě na kole.
Kalkulačka Pravděpodobnosti čeština
Zveřejněno: Sun Jan 08 2023
V kategorii Matematické kalkulačky
Přidejte Kalkulačka Pravděpodobnosti na svůj vlastní web