Matematikai Számológépek
Valószínűség-kalkulátor
A valószínűség-kalkulátor segítségével feltárhatja a valószínűségi összefüggéseket két különálló esemény között. Ez lehetővé teszi, hogy jobban megértse, hogyan kapcsolódnak egymáshoz az események, és ezáltal pontosabbak az előrejelzések.
Egyedi események valószínűsége
%
%
Melyik valószínűséget szeretné látni?
%
Egy eseménysorozat valószínűségei
alkalommal
%
Tartalomjegyzék
| ◦Valószínűség meghatározása |
| ◦Feltételes valószínűség |
| ◦Elméleti vs kísérleti valószínűség |
| ◦Valószínűség és statisztika |
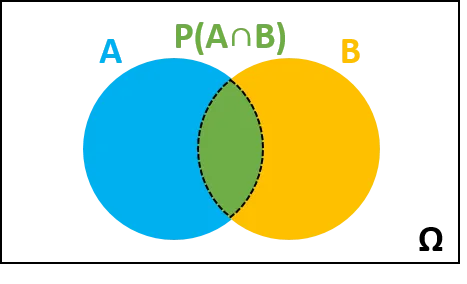
A valószínűség-kalkulátor hasznos eszköz az események közötti összefüggések vizsgálatához, mint például A bekövetkezésének esélye és B bekövetkezésének esélye. Például, ha az esélye, hogy A megtörténik, 50%, és ugyanez B-re, mennyi az esélye annak, hogy mindkettő megtörténik, csak az egyik történik, legalább az egyik megtörténik, vagy egyik sem, és így tovább?
Valószínűség-kalkulátorunk hat különböző forgatókönyv valószínűségét segíti. Ráadásul, ha megadja, hogy hányszor van a "kockával dobva", akkor további négy forgatókönyvet kínál. Így nem kell minden számítást magának elvégeznie. Csak írja be a számokat, és a többiről kalkulátorunk gondoskodik!
Valószínűség meghatározása
A valószínűség egy gondolkodásmód a bizonytalan helyzetekről, és számos területen használják, például a szerencsejátékban, a döntéshozatalban és a statisztikákban. A valószínűség definíciója ebben a kurzusban a tantárgy legalapvetőbb és legalapvetőbb definíciója.
Feltételes valószínűség
A valószínűség a véletlen tanulmányozásáról szól, és az egyik legfontosabb megértendő fogalom az, hogy az események függőek-e vagy sem. Két esemény független, ha az első bekövetkezése nem befolyásolja a második bekövetkezésének valószínűségét. Ez hihetetlenül fontos, mert ez határozza meg, hogyan számíthatjuk ki a lehetséges eredményeket. Ha egy tökéletesen kiegyensúlyozott normál köbös kockával dobunk, 1/6 az esélye, hogy kettőt kapunk.
Annak ellenére, hogy ebben a példában a kockákat összekapcsoltuk, annak a valószínűsége, hogy a második körben kettőt kapunk, még mindig 1/6, mivel az események függetlenek. Ez azt jelenti, hogy annak valószínűsége, hogy legalább egy konkrét eredményt, például kettőt ⚁ kapunk az első körben, nem függ attól, hogy mi történik a kockával a második körben.
Valószínűleg különböző módokon lehet egy forgatókönyvet megvizsgálni. Ezúttal a feltételes valószínűségről fogunk beszélni. Tegyük fel, hogy teniszjátékot játszol, és az egyik ellenfeled közeledik a hálóhoz. Attól függően, hogy milyen szögben ütik el a labdát, lehetséges, hogy egy lövéssel elküldik a labdát az ellenfél mellett. Ha azonban ellenfelük kacsázik, amikor látja, hogy jön a labda, a labda valószínűleg felpattan a földről, és az ellenfél elkaphatja. Ez egy példa arra a helyzetre, amikor a játékról az eseményekben (labdaütés) és az eredményekben gondolkodunk.
Elméleti vs kísérleti valószínűség
A legtöbb esetben az elméleti valószínűséget a kedvező kimenetelek száma és az összes lehetséges kimenetel számának arányaként határozzák meg. Van azonban különbség az elméleti valószínűség és a kísérleti valószínűség között. A kísérleti valószínűség formális definíciója az egy adott kategóriába (a kísérlet) tartozó eredmények számának és az eredmények teljes számának aránya. A kísérlet tervezése a megadott információkra, logikus érvelésre támaszkodik, és megmondja, mit várhatunk a kísérlettől. Ideális esetben ez az információ a tesztelt hipotézisből származik. Ezen információk összegyűjtése után a kísérleti terv segít a kísérlet olyan megtervezésében, amely igazolja vagy érvényteleníti hipotézisét.
A 42 golyós játékban véletlenszerűen kiválasztanak egy labdát, és végtelen számú alkalommal visszateszik a zacskóba. Ez azt jelenti, hogy mindig 42 golyó van a zacskóban, ebből 18 narancssárga. Kiszámíthatjuk egy adott szín kiválasztásának valószínűségét, ha elosztjuk az adott színű golyók számát a zsákban lévő golyók számával (42). Ezt 3/7-re egyszerűsítjük, vagy a valószínűség 18/42, ami azt jelenti, hogy minden 14 felszedett golyóból 3 narancssárga golyónak kell lennie.
A valószínűség egy matematikai tudomány, amely annak a lehetőségével foglalkozik, hogy valami megtörténjen. Használható arra, hogy megjósolja, mi fog történni egy kísérlet végrehajtása eredményeként, vagy annak megértésére, hogy egy adott helyzetben valami megtörténhet. Ebben a példában a kísérleti valószínűséget fogjuk használni, hogy megértsük, mi történt, amikor kivettünk egy márványt egy zacskóból, és még 13-szor megismételtük az eljárást. Tegyük fel, hogy 8 narancssárga golyót kaptunk 14 kísérletben. Ez 14-ből 8, azaz 44%-os empirikus valószínűséget ad nekünk.
Lesz idő, amikor több kártyát választ, időnként kevesebbet kap, és lesz, amikor a megjósolt számot választja. Az eredmény azonban eltér az elméletitől. Ez azért van így, mert amikor megpróbálod újra és újra megismételni ezt a játékot, néha többet választasz, néha pedig kevesebbet, néha pedig pontosan az elméletileg megjósolt számot választod. Ha az összes eredményt összegzi, észre kell vennie, hogy az általános valószínűség egyre közelebb kerül az elméleti valószínűséghez. Ha nem, akkor eltérés lehet a látott és a feltételezett eredmény között – ez lehet a helyzet például akkor, ha a zsákban lévő golyók különböző színűek és méretűek. A pontos becslés érdekében a kiválasztási folyamatot véletlenszerűen kell kiválasztani.
Valószínűség és statisztika
A statisztika a matematikának az adatok gyűjtésével, értelmezésével, elemzésével, bemutatásával és értelmezésével foglalkozó ága. A valószínűségszámítás a matematikának az az ága, amely az események lehetőségét és annak kimenetelét vizsgálja. Fontos megérteni ezeket a különbségeket, mivel különböző helyzetekben eltérő következtetésekhez vezethetnek.
A valószínűségszámítás a matematikának egy olyan elméleti területe, amely olyan dolgokkal foglalkozik, mint a matematikai definíciók és tételek. Ezzel szemben a statisztika a matematika gyakorlati alkalmazása, amely megpróbálja a valós világban megfigyelések értelmét és megértését tulajdonítani. A statisztikák két fő ágra oszthatók - leíró és következtetéses. A leíró statisztika egy sokaság leíró tulajdonságait vizsgálja, mint például a számok, az átlagok és a szórások. A következtetési statisztika statisztikai módszerekkel von le következtetéseket egy populációról mintákból, akár kísérletekből, akár a való világból vett megfigyelésekből.
A valószínűség az események lehetőségének előrejelzésének képessége, míg a statisztika a múltbeli események gyakoriságának vizsgálata. A tanfolyam végére mélyebben megérti ezeket a fogalmakat, és képes lesz használni őket valós adatok modellezésére.
Tegyük fel, hogy egy szerencsejátékot játszol, ahol minden kártya azonos valószínűséggel kerül kiválasztásra, és a célod a győzelem. Ebben az esetben tétet köthet az oddsok alapján – vagyis annak a valószínűsége alapján, hogy a választott lap ásó lesz. Feltételezve, hogy a pakli teljes, és a választás teljesen véletlenszerű és méltányos, akkor arra következtethet, hogy a valószínűség egyenlő ¼-vel. Ez azt jelenti, hogy magabiztosan fogadhat.
Egy statisztikus egy ideig figyeli a játékot, hogy felmérje a tisztességességet, mielőtt konzultál a valószínűségszámítóval arról, hogy milyen lépéseket kell tennie, hogy a legnagyobb esélye legyen a győzelemre. Miután megállapodtak abban, hogy megéri a játékot játszani, a valószínűségszámító tanácsot ad, milyen lépéseket tegyenek esélyeik javítása érdekében.
A cikk szerzője
John Cruz
John PhD -hallgató, aki rajong a matematikáért és az oktatásért. Szabadidejében John szeret túrázni és kerékpározni.
Valószínűség-kalkulátor magyar nyelv
Közzétett: Sun Jan 08 2023
A (z) Matematikai számológépek kategóriában
A (z) Valószínűség-kalkulátor hozzáadása saját webhelyéhez