Matematikai Számológépek
Trigonometrikus Számológép
Számítsa ki egyszerűen a Sin, Cos, Tan, Cot, Sec és Csc trigonometrikus értékeket ingyenes online számológépünkkel!
Trigonometrikus számológép
Tartalomjegyzék
Mi az a trigonometria?
A trigonometria a matematikának egy ága, amely a háromszög oldalaival és szögeivel foglalkozik. Ez a témakör a szögszámításhoz használt releváns függvényeket is lefedi.
Melyek az elsődleges vagy alapvető trigonometrikus függvények?
Az alábbiakban az elsődleges trigonometrikus függvények listája látható, amelyeket főként a trigonometria használatakor használnak.
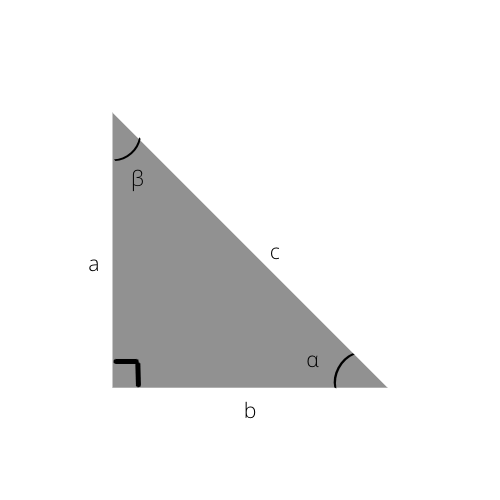
Példa derékszögű háromszögre. A képen látható "α" szögre a következő képletek hivatkoznak.
1) Szög szinusza
Képlet: sin α = ellentétes / hipotenusz
Egy szög szinuszának aránya derékszögű háromszög esetén az ellentét hosszának osztva a befogó hosszával.
2) Szög koszinusza
Képlet: cos α = szomszédos / hipotenusz
Egy derékszögű háromszög összefüggésében egy szög koszinuszát úgy számítjuk ki, hogy a szomszédos hosszát elosztjuk a befogó hosszával.
3) Szög érintője
Képlet: tan α = sin α / cos α = szemközti / szomszédos
A derékszögű háromszögben egy szög érintőjét úgy számítjuk ki, hogy a szinust elosztjuk a koszinusszal. Ez helyettesíthető úgy is, hogy az ellenkezőjét elosztjuk a szomszédossal.
Ezen függvények használatakor ne feledje a trigonometrikus táblázatot is.
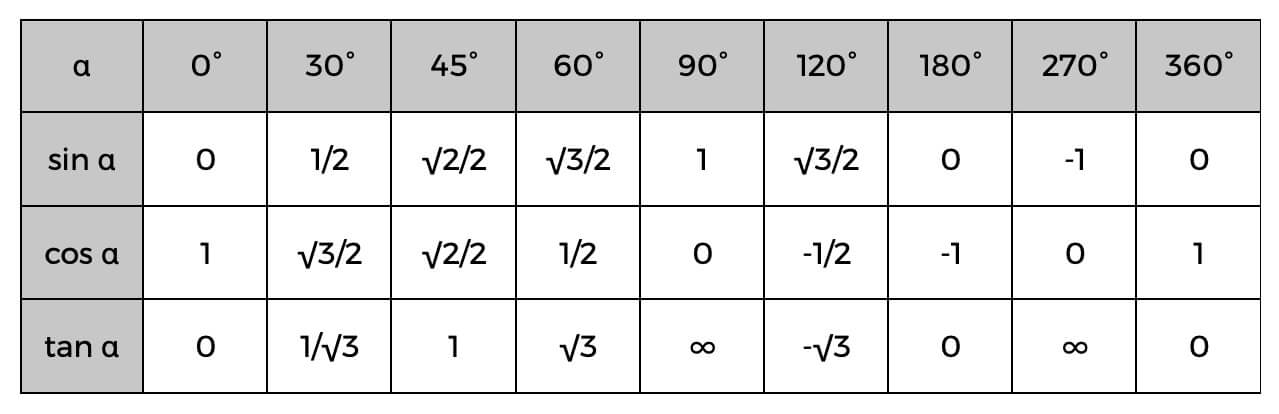
A trigonometrikus táblázat
Mik azok a reciprok trigonometrikus függvények?
Az elsõdleges trigonometrikus függvények mellett van egy másik függvénykészlet is, amelyek az elsõ kategóriához képest nem használtak. Ide tartozik a szekáns (sec), a koszekáns (csc) és a kotangens (cot).
Mire használják a trigonometriát?
A trigonometria a háromszögekhez, különösen a derékszögű háromszögekhez kapcsolódik. Tehát bárhol lát egy háromszöget a matematika világán kívül, fogadjon, hogy a trigonometria hasznos. Példa erre a trigonometrikus számítások alkalmazása olyan területeken, mint az építészet, a csillagászat és a vegyészmérnökök.
A trigonometria valós alkalmazásai
A matematikában használatos trigonometria nyilvánvaló használatán kívül a trigonometriát valós helyzetekben és területeken is használják.
1) Építészet és mérnöki tudomány
Nem túl messzire gondolunk a trigonometrikus függvények építészetben való használatára. Ezeket a függvényeket leginkább a két vonalat összekötő átlós kapcsolat hosszának kiszámítására használják. Ezt használják a tető lejtésének átlós hosszának kiszámításához lejtős tető tervezésekor. Csak a tető magasságát és hosszát kellene ismernie, és már indulhat is!

2) Csillagászat
A csillagászat olyan fontos téma, amelyre a régi kultúrák leginkább figyeltek. Ha erről beszélünk, valószínűleg az egyik első dolog, ami eszünkbe jut, az a csillagképek, és ezek távolságának kiszámítása egymástól és más űrbeli objektumoktól, ami a csillagászat egyik egyszerűbb felhasználási módja. Más szóval, a trigonometria segítségével kiszámítható a Nap és a Föld távolsága a különböző csillagoktól. A csillagok távolsága fontos tényezőik kiszámításához a csillagászat világában.
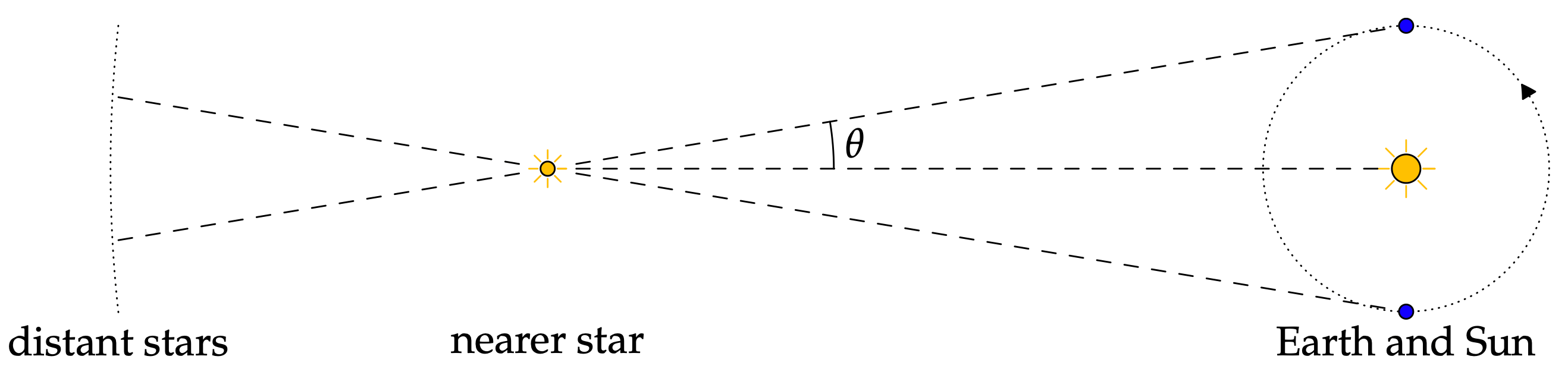
Tekintse meg ezt a cikket további információkért a csillagászatról és annak a trigonometriával való kapcsolatáról:
3) Elektronika és elektrotechnika
A trigonometriát az elektronikai és elektrotechnikai matematikai problémák megoldására használják, leginkább modelltervezéskor. Egy másik példa a fontosságra az esztétikai kiegészítések elvégzése, és annak biztosítása, hogy azok ne zavarják a modell működését.
A trigonometrikus függvények azonban nagyon hasznosak az áramkörökkel végzett munka során. Tekintse meg az alábbi vizuális példát a további demonstrációhoz, és hogy képet kapjon arról, hogy a trigonometria hogyan válik áramköri logikává.
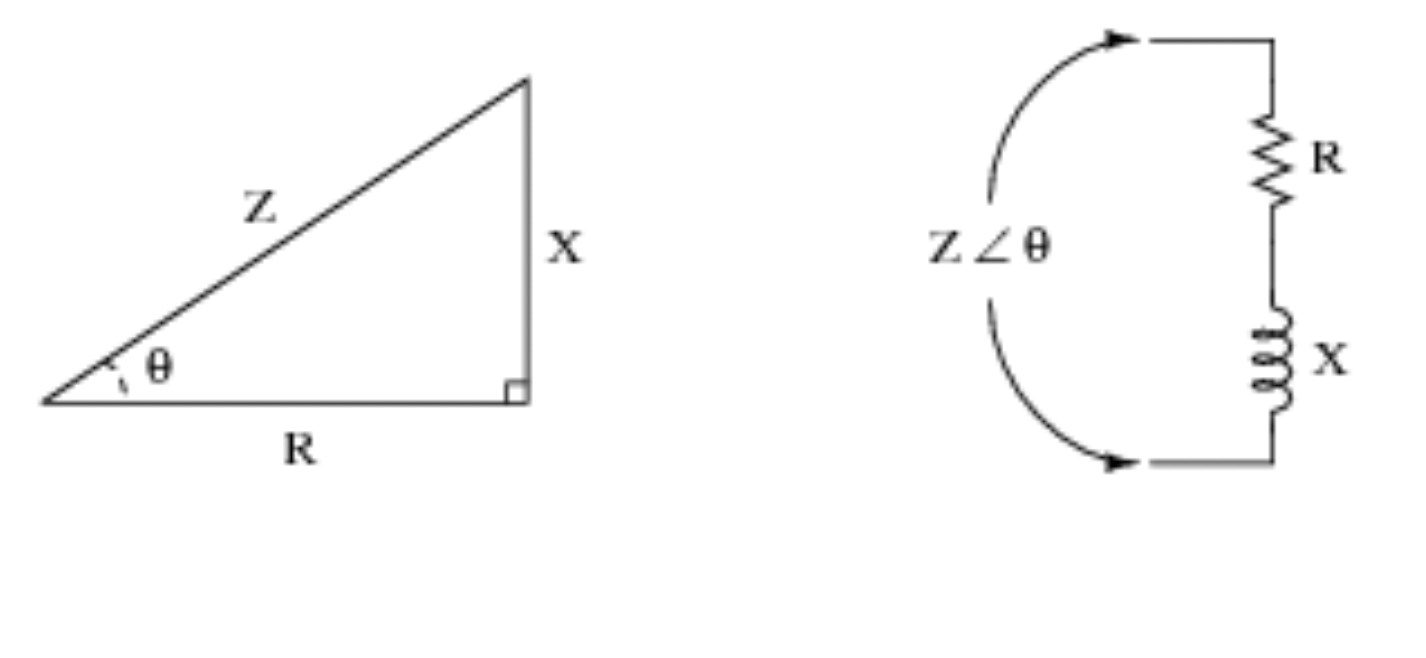
4) Szeizmológia
A szeizmológia a földrengések, valamint a földön át és körülötte mozgó szeizmikus hullámok tanulmányozása. A trigonometria megkönnyíti a szeizmikus hullám által megtett függőleges és vízszintes távolság kiszámítását.

5) Földmérés (mélyépítés)
A földmérési szakma már régóta létezik, legalábbis addig, amíg a feljegyzett történelem mutatja. Ezt egy földmérő végzi, akinek az a feladata, hogy nagy léptékben pontosan megmérje a Föld felszínét. Talán már sejtette a trigonometria használatát; alapvetően a trigonometria akkor jön be, ha a földmérőnek ki kell számítania a tájon lévő objektumok hosszát, területeit és relatív szögeit.
Az alábbi példa jól szemlélteti a korábban leírtakat. A földmérő trigonometrikus törtszámok segítségével számítja ki saját távolságát a hegycsúcstól vagy bárhonnan, amelyet választott.

A cikk szerzője
Parmis Kazemi
Parmis tartalomkészítő, aki szenvedélyesen ír és új dolgokat hoz létre. Nagyon érdekli a technika és szívesen tanul új dolgokat.
Trigonometrikus Számológép magyar nyelv
Közzétett: Fri Oct 29 2021
A (z) Matematikai számológépek kategóriában
A (z) Trigonometrikus Számológép hozzáadása saját webhelyéhez