Matematiske Kalkulatorer
Trigonometrikalkulator
Beregn enkelt trigonometriske verdier Sin, Cos, Tan, Cot, Sec og Csc med vår gratis online kalkulator!
Trigonometrikalkulator
Innholdsfortegnelse
Hva er trigonometri?
Trigonometri er en gren av matematikken som omhandler sidene og vinklene i en trekant. Dette emnet dekker også de relevante funksjonene som brukes for beregning av vinkler.
Hva er de primære eller grunnleggende trigonometriske funksjonene?
Nedenfor vil du se en liste over de primære trigonometriske funksjonene som hovedsakelig brukes ved bruk av trigonometri.
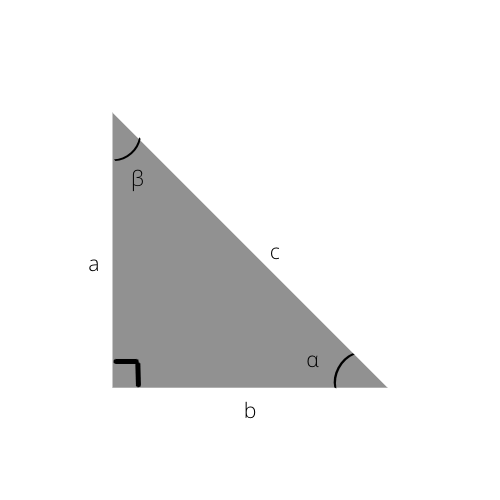
Et eksempel på en rettvinklet trekant. "α"-vinkelen i dette bildet er referert til i følgende formler.
1) Sinus av en vinkel
Formel: sin α = motsatt / hypotenusen
Forholdet mellom sinusen til en vinkel, i sammenheng med en rettvinklet trekant, er lengden av det motsatte delt på lengden på hypotenusen.
2) Cosinus av en vinkel
Formel: cos α = tilstøtende / hypotenuse
Cosinus til en vinkel, i sammenheng med en rettvinklet trekant, beregnes ved å dele lengden av den tilstøtende med lengden på hypotenusen.
3) Tangent av en vinkel
Formel: tan α = sin α / cos α = motsatt / tilstøtende
Tangensen til en vinkel, i sammenheng med en rettvinklet trekant, beregnes ved å dele sinusen med cosinus. Dette kan også erstattes ved å dele det motsatte med det tilstøtende.
Husk også den trigonometriske tabellen når du bruker disse funksjonene.
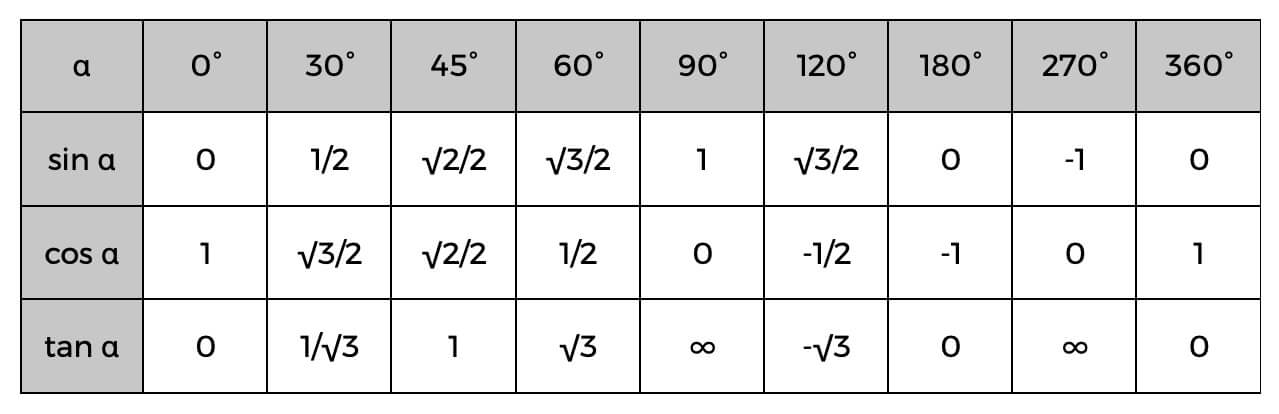
Den trigonometriske tabellen
Hva er gjensidige trigonometriske funksjoner?
Foruten de primære trigonometriske funksjonene, er det også et annet sett med funksjoner som ikke er like brukt sammenlignet med den første kategorien. Disse inkluderer secant (sec), cosecant (csc) og cotangens (cot).
Hva brukes trigonometri til?
Trigonometri er relatert til trekanter, spesielt rette trekanter. Så uansett hvor du ser en trekant utenfor matematikkverdenen, satser du på at trigonometri er nyttig. Et eksempel på dette er bruken av trigonometriske beregninger innen felt som arkitektur, astronomi og kjemiteknikk.
Virkelige anvendelser av trigonometri
Annet enn den åpenbare bruken av trigonometri, som er i matematikk, brukes trigonometri også i virkelige situasjoner og felt.
1) Arkitektur og ingeniørfag
Det er ikke så langt unna å tenke på bruken av trigonometriske funksjoner i arkitektur. Disse funksjonene brukes mest til å beregne lengden på diagonalforbindelsen som forbinder to linjer. Dette brukes til å beregne diagonallengden på et taks skråning ved utforming av et skråtak. Du trenger bare å vite høyden og lengden på taket, og du er i gang!

2) Astronomi
Astronomi er et viktig fag som gamle kulturer stort sett ga oppmerksomhet til. Når man snakker om dette, er sannsynligvis en av de første tingene som kommer til tankene stjernebildene og beregningen av deres avstand fra hverandre og andre objekter i rommet, som er en av de mer enkle bruksområdene for astronomi. Med andre ord kan trigonometri brukes til å beregne avstanden mellom solen og jorden fra forskjellige stjerner. Avstanden til stjernene er viktig for å beregne deres faktorer i astronomiens verden.
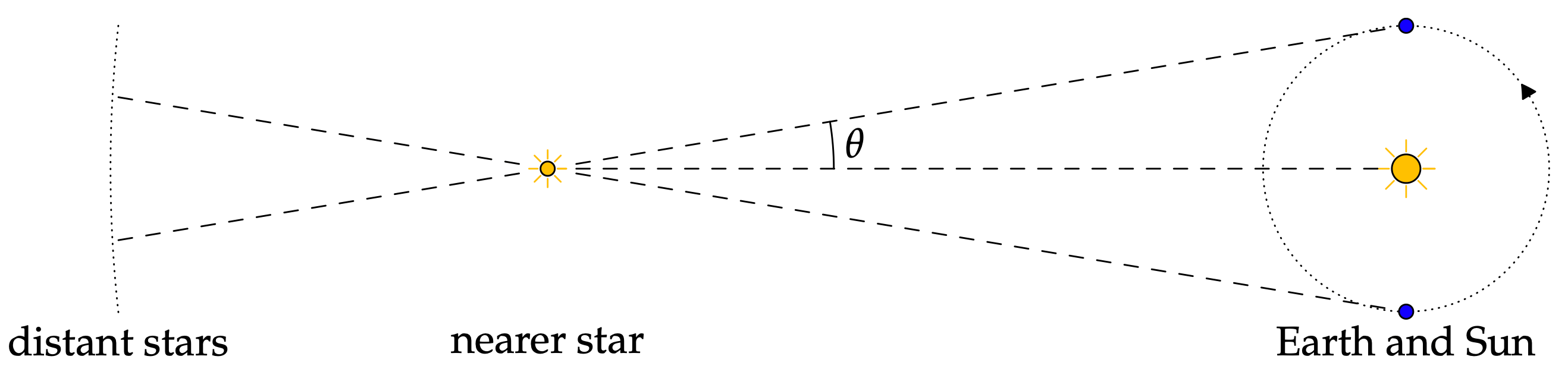
Se denne artikkelen for mer informasjon om astronomi og dens forhold til trigonometri:
3) Elektronikk og elektroteknikk
Trigonometri brukes til å løse matematiske problemer innen elektronikk og elektroteknikk, mest når man designer en modell. Et annet eksempel på viktigheten er når man gjør estetiske tillegg og sørger for at de ikke forstyrrer modellens funksjon.
Imidlertid er trigonometriske funksjoner veldig nyttige når du arbeider med kretser. Se det visuelle eksemplet nedenfor for ytterligere demonstrasjon og for å få en ide om hvordan trigonometri oversettes til kretslogikk.
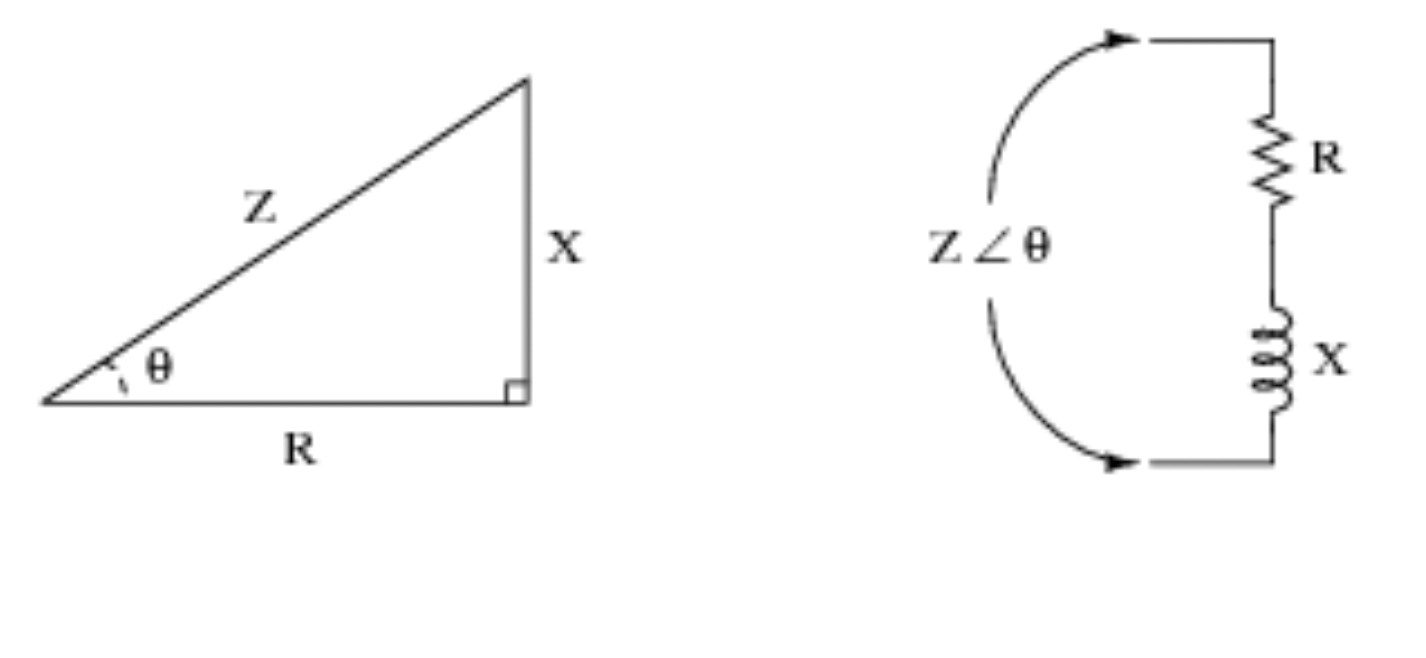
4) Seismologi
Seismologi er læren om jordskjelv, så vel som de seismiske bølgene som beveger seg gjennom og rundt jorden. Trigonometri kommer inn for å lette beregningen av den vertikale og horisontale avstanden en seismisk bølge reiser.

5) Landmåling (anleggsteknikk)
Oppmåling har vært et yrke som har eksistert lenge, i alle fall så lenge nedtegnet historie viser. Dette gjøres av en landmåler som har jobben med å nøyaktig måle jordoverflatene i stor skala. Du har kanskje gjettet bruken av trigonometri nå; i utgangspunktet kommer trigonometri inn når landmåleren trenger å beregne lengden, arealene og relative vinklene mellom objektene i landskapet.
Eksemplet nedenfor er en god visuell demonstrasjon av det som tidligere er forklart. En landmåler bruker trigonometriske brøker for å beregne sin egen avstand fra fjelltoppen eller fra et annet sted de velger.

Artikkelforfatter
Parmis Kazemi
Parmis er en innholdsskaper som har en lidenskap for å skrive og skape nye ting. Hun er også sterkt interessert i teknologi og liker å lære nye ting.
Trigonometrikalkulator Norsk
Publisert: Fri Oct 29 2021
I kategori Matematiske kalkulatorer
Legg til Trigonometrikalkulator på ditt eget nettsted