Kalkulatory Matematyczne
Kalkulator Trygonometrii
Łatwe obliczanie wartości trygonometrycznych Sin, Cos, Tan, Cot, Sec i Csc za pomocą naszego bezpłatnego kalkulatora online!
Kalkulator trygonometrii
Spis treści
| ◦Czym jest trygonometria? |
| ◦Jakie są podstawowe lub podstawowe funkcje trygonometryczne? |
| ◦Czym są odwrotne funkcje trygonometryczne? |
| ◦Do czego służy trygonometria? |
| ◦Rzeczywiste zastosowania trygonometrii |
Czym jest trygonometria?
Trygonometria to dział matematyki zajmujący się bokami i kątami w trójkącie. Temat ten obejmuje również odpowiednie funkcje używane do obliczania kątów.
Jakie są podstawowe lub podstawowe funkcje trygonometryczne?
Poniżej zobaczysz listę podstawowych funkcji trygonometrycznych, które są używane głównie podczas korzystania z trygonometrii.
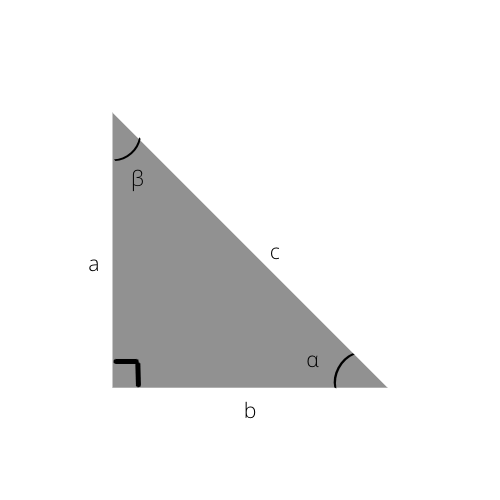
Przykład trójkąta prostokątnego. Poniższe wzory odnoszą się do kąta „α” na tym obrazie.
1) Sinus kąta
Wzór: sin α = przeciwna / przeciwprostokątna
Stosunek sinusa kąta w kontekście trójkąta prostokątnego to długość przeciwnej strony podzielona przez długość przeciwprostokątnej.
2) Cosinus kąta
Wzór: cos α = sąsiednie / przeciwprostokątna
Cosinus kąta w kontekście trójkąta prostokątnego oblicza się dzieląc długość sąsiedniego kąta przez długość przeciwprostokątnej.
3) Styczna do kąta
Wzór: tan α = sin α / cos α = przeciwnie / przyległe
Tangens kąta w kontekście trójkąta prostokątnego oblicza się dzieląc sinus przez cosinus. Można to również zastąpić, dzieląc przeciwieństwo przez sąsiednie.
Należy również pamiętać o tabeli trygonometrycznej podczas korzystania z tych funkcji.
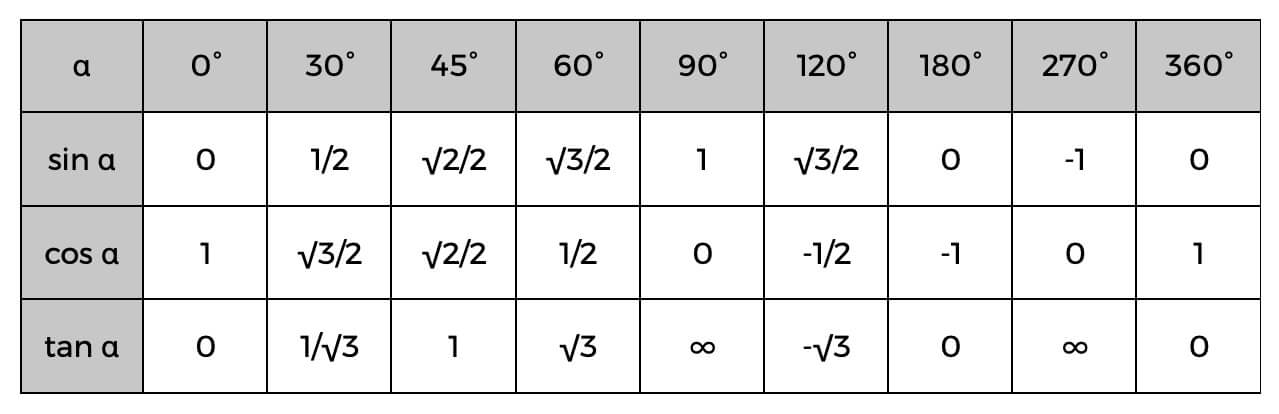
Stół trygonometryczny
Czym są odwrotne funkcje trygonometryczne?
Oprócz podstawowych funkcji trygonometrycznych istnieje również inny zestaw funkcji, które nie są używane w porównaniu z pierwszą kategorią. Należą do nich sieczna (sec), cosecans (csc) i cotangens (cot).
Do czego służy trygonometria?
Trygonometria dotyczy trójkątów, w szczególności trójkątów prostokątnych. Tak więc, gdziekolwiek widzisz trójkąt poza światem matematyki, możesz się założyć, że trygonometria jest pomocna. Przykładem tego jest zastosowanie obliczeń trygonometrycznych w dziedzinach takich jak architektura, astronomia i inżynieria chemiczna.
Rzeczywiste zastosowania trygonometrii
Poza oczywistym użyciem trygonometrii, która jest w matematyce, trygonometria jest również używana w sytuacjach i dziedzinach życia codziennego.
1) Architektura i inżynieria
Nie jest zbyt daleko, by pomyśleć o wykorzystaniu funkcji trygonometrycznych w architekturze. Funkcje te są najczęściej używane do obliczania długości połączenia ukośnego łączącego dwie linie. Służy do obliczania długości przekątnej połaci dachu podczas projektowania dachu pochyłego. Wystarczy znać wysokość i długość dachu i gotowe!

2) Astronomia
Astronomia to ważny temat, na który w większości zwracały uwagę dawne kultury. Mówiąc o tym, prawdopodobnie jedną z pierwszych rzeczy, które przychodzą na myśl, są konstelacje i obliczanie ich odległości od siebie i innych obiektów w przestrzeni, co jest jednym z prostszych zastosowań astronomii. Innymi słowy, trygonometrii można użyć do obliczenia odległości Słońca i Ziemi od różnych gwiazd. Odległość gwiazd jest ważna dla obliczania ich współczynników w świecie astronomii.
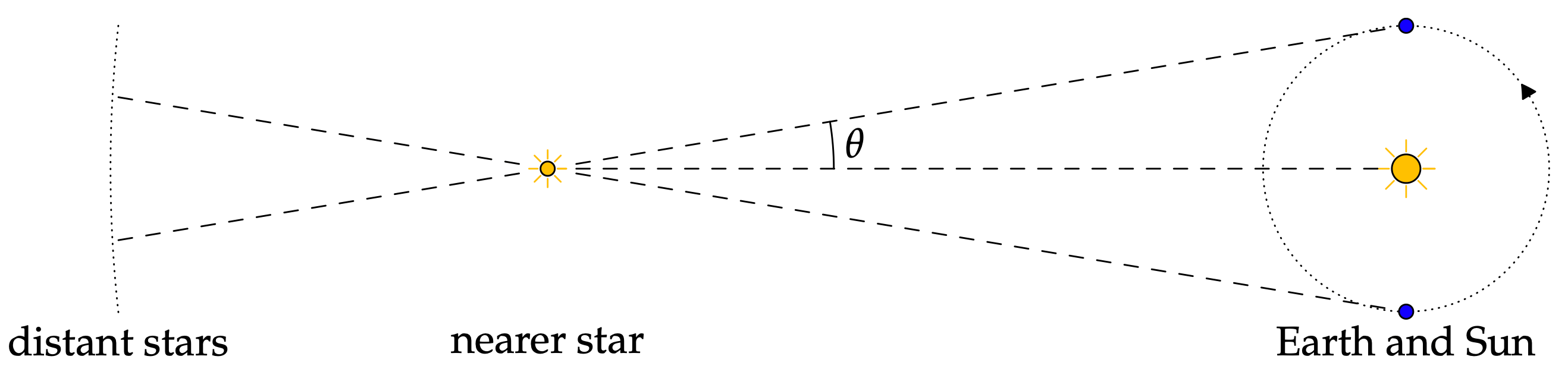
Zobacz ten artykuł, aby uzyskać więcej informacji na temat astronomii i jej związku z trygonometrią:
3) Elektronika i elektrotechnika
Trygonometria służy do rozwiązywania problemów matematycznych w elektronice i elektrotechnice, głównie podczas projektowania modelu. Innym przykładem tego, jak ważne jest wykonanie estetycznych dodatków i upewnienie się, że nie zaburzają funkcji modelu.
Jednak funkcje trygonometryczne są bardzo przydatne podczas pracy z obwodami. Zobacz poniższy wizualny przykład, aby uzyskać dalszą demonstrację i zorientować się, jak trygonometria przekłada się na logikę obwodu.
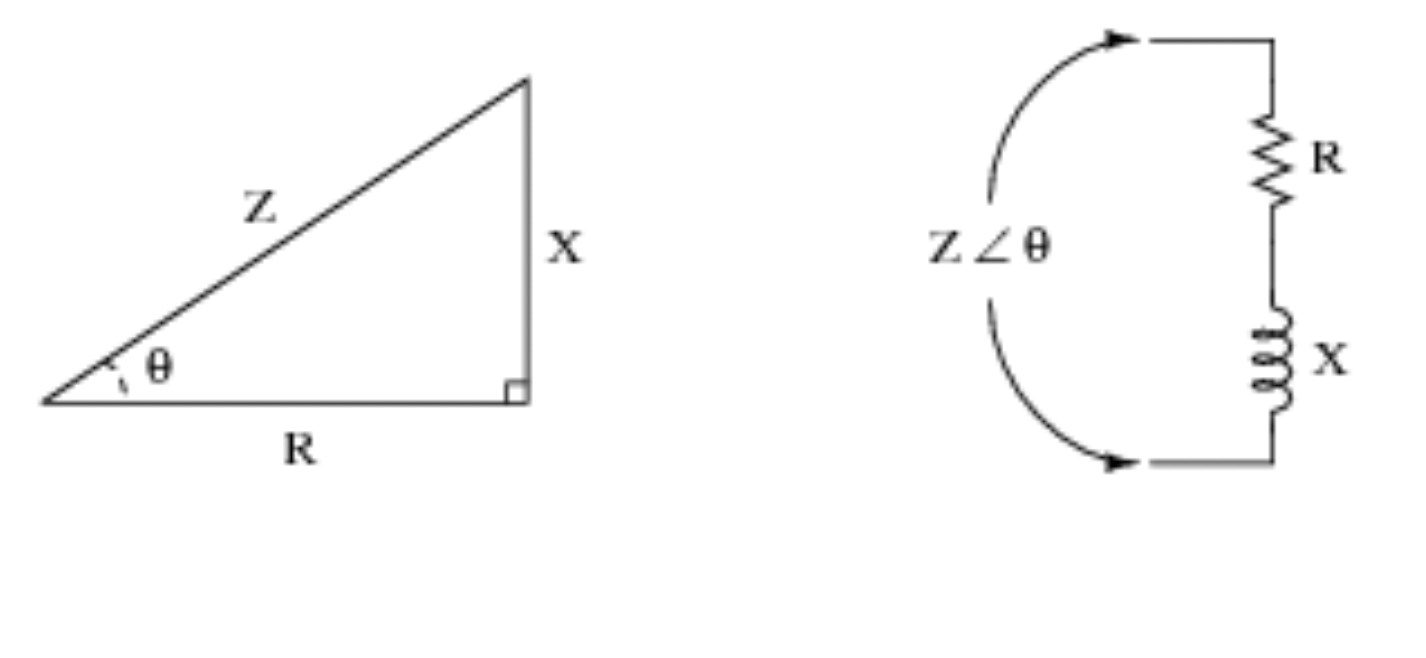
4) Sejsmologia
Sejsmologia zajmuje się badaniem trzęsień ziemi, a także fal sejsmicznych, które poruszają się po Ziemi i wokół niej. Trygonometria ułatwia obliczanie odległości w pionie i poziomie, jaką przebyła fala sejsmiczna.

5) Geodezja (inżynieria lądowa)
Geodezja to zawód, który istnieje od dawna, przynajmniej tak długo, jak pokazuje historia. Dokonuje tego geodeta, którego zadaniem jest dokładne mierzenie powierzchni Ziemi na dużą skalę. Być może już domyśliłeś się zastosowania trygonometrii; w zasadzie trygonometria pojawia się, gdy geodeta musi obliczyć długość, obszary i względne kąty między obiektami na krajobrazie.
Poniższy przykład jest dobrym wizualnym demonstratorem tego, co zostało wcześniej wyjaśnione. Geodeta używa ułamków trygonometrycznych do obliczania własnej odległości od szczytu góry lub dowolnego innego miejsca, które wybierze.

Autor artykułu
Parmis Kazemi
Parmis to twórca treści, który ma pasję do pisania i tworzenia nowych rzeczy. Jest również bardzo zainteresowana technologią i lubi uczyć się nowych rzeczy.
Kalkulator Trygonometrii Polski
Opublikowany: Fri Oct 29 2021
W kategorii Kalkulatory matematyczne
Dodaj Kalkulator Trygonometrii do własnej witryny