Riyazi Hesablayıcılar
Triqonometriya Kalkulyatoru
Pulsuz onlayn kalkulyatorumuzla Sin, Cos, Tan, Cot, Sec və Csc triqonometrik dəyərlərini asanlıqla hesablayın!
Triqonometriya kalkulyatoru
Mündəricat
Triqonometriya nədir?
Triqonometriya üçbucağın tərəfləri və bucaqları ilə məşğul olan riyaziyyatın bir sahəsidir. Bu mövzu həmçinin bucaqların hesablanması üçün istifadə olunan müvafiq funksiyaları əhatə edir.
Əsas və ya əsas triqonometrik funksiyalar hansılardır?
Aşağıda triqonometriyadan istifadə edərkən əsasən istifadə olunan əsas triqonometrik funksiyaların siyahısını görəcəksiniz.
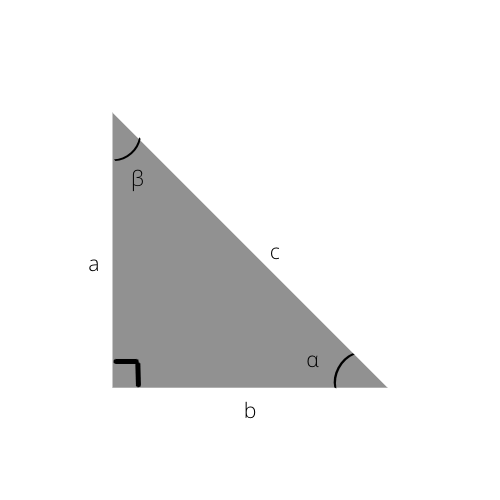
Düzbucaqlı üçbucağın nümunəsi. Bu şəkildəki "α" bucağı aşağıdakı düsturlarda istinad edilir.
1) Bucağın sinusu
Formula: sin α = əks / hipotenuz
Düzbucaqlı üçbucaq kontekstində bucağın sinusunun nisbəti əks tərəfin uzunluğunun hipotenuzanın uzunluğuna bölünməsidir.
2) Bucağın kosinusu
Formula: cos α = bitişik / hipotenuz
Düzbucaqlı üçbucağın kontekstində bir bucağın kosinusu, qonşunun uzunluğunu hipotenuzanın uzunluğuna bölmək yolu ilə hesablanır.
3) Bucağın tangensi
Formula: tan α = sin α / cos α = əks / bitişik
Düzbucaqlı üçbucaq kontekstində bucağın tangensi sinusun kosinusu ilə bölünməsi ilə hesablanır. Bu, əksini qonşuya bölmək yolu ilə də əvəz edilə bilər.
Bu funksiyalardan istifadə edərkən triqonometrik cədvəli də unutmayın.
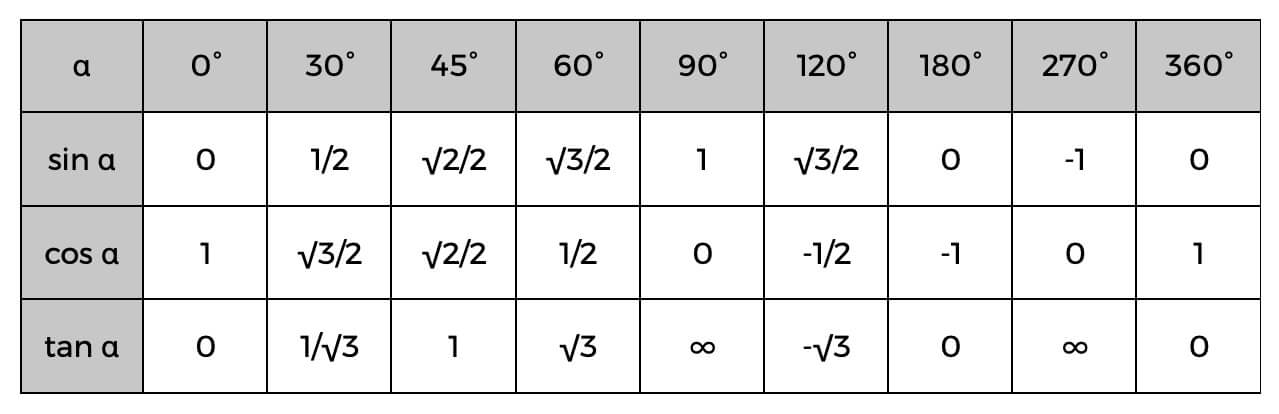
Triqonometrik cədvəl
Qarşılıqlı triqonometrik funksiyalar hansılardır?
Əsas triqonometrik funksiyalardan başqa, birinci kateqoriya ilə müqayisədə istifadə olunmayan başqa bir funksiya dəsti var. Bunlara sekant (san), kosekant (csc) və kotangent (beşik) daxildir.
Triqonometriya nə üçün istifadə olunur?
Triqonometriya üçbucaqlarla, xüsusən də düzbucaqlı üçbucaqlarla bağlıdır. Beləliklə, riyaziyyat dünyasından kənarda üçbucaq görsəniz, triqonometriyanın faydalı olduğuna mərc edərsiniz. Buna misal olaraq memarlıq, astronomiya və kimya mühəndisliyi kimi sahələrdə triqonometrik hesablamalardan istifadə etmək olar.
Triqonometriyanın real həyatda tətbiqi
Riyaziyyatda olan triqonometriyanın aşkar istifadəsi ilə yanaşı, triqonometriya da real həyat vəziyyətlərində və sahələrdə istifadə olunur.
1) Memarlıq və mühəndislik
Memarlıqda triqonometrik funksiyaların istifadəsi haqqında düşünmək çox da uzaqda deyil. Bu funksiyalar əsasən iki xətti birləşdirən diaqonal əlaqənin uzunluğunu hesablamaq üçün istifadə olunur. Bu, yamaclı bir damın layihələndirilməsi zamanı damın yamacının diaqonal uzunluğunu hesablamaq üçün istifadə olunur. Yalnız damın hündürlüyünü və uzunluğunu bilmək lazımdır və getməyə hazırsınız!

2) Astronomiya
Astronomiya qədim mədəniyyətlərin daha çox diqqət yetirdiyi mühüm bir mövzudur. Bundan danışarkən, yəqin ki, ilk ağıla gələn şeylərdən biri astronomiyanın daha sadə istifadələrindən biri olan bürclər və onların bir-birindən və kosmosdakı digər cisimlərdən məsafəsinin hesablanmasıdır. Başqa sözlə desək, triqonometriya ilə günəşlə yerin müxtəlif ulduzlardan məsafəsini hesablamaq olar. Ulduzların uzaqlığı astronomiya aləmində onların faktorlarını hesablamaq üçün vacibdir.
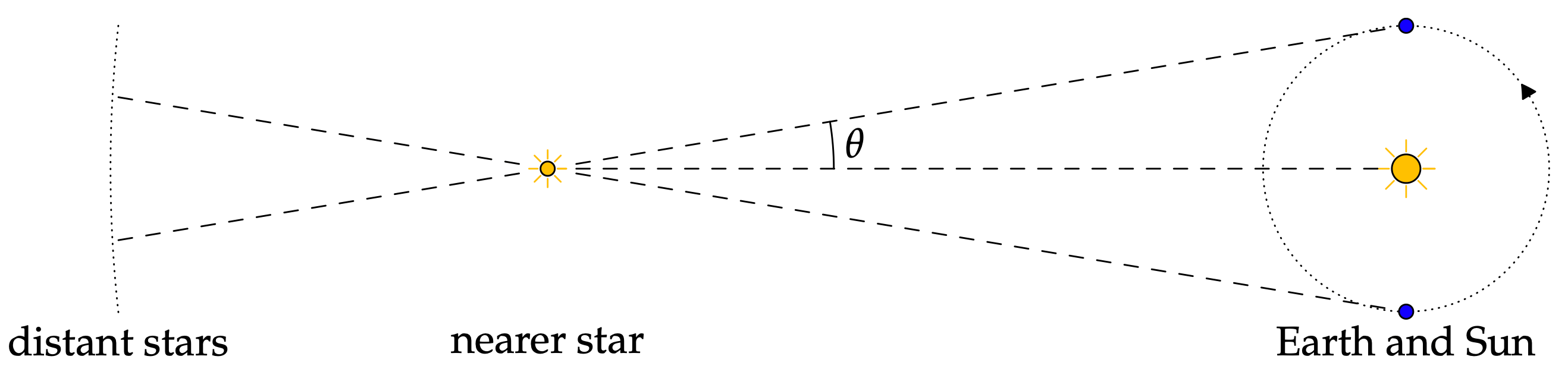
Astronomiya və onun triqonometriya ilə əlaqəsi haqqında əlavə məlumat üçün bu məqaləyə baxın:
3) Elektronika və elektrik mühəndisliyi
Triqonometriya elektronika və elektrik mühəndisliyində riyaziyyat problemlərinin həlli üçün, əsasən modelin layihələndirilməsi zamanı istifadə olunur. Əhəmiyyətin başqa bir nümunəsi estetik əlavələr edərkən və onların modelin funksiyasını pozmadığından əmin olmaqdır.
Bununla belə, triqonometrik funksiyalar sxemlərlə işləyərkən çox faydalıdır. Əlavə nümayiş etdirmək və triqonometriyanın dövrə məntiqinə necə çevrildiyi barədə fikir əldə etmək üçün aşağıdakı vizual nümunəyə baxın.
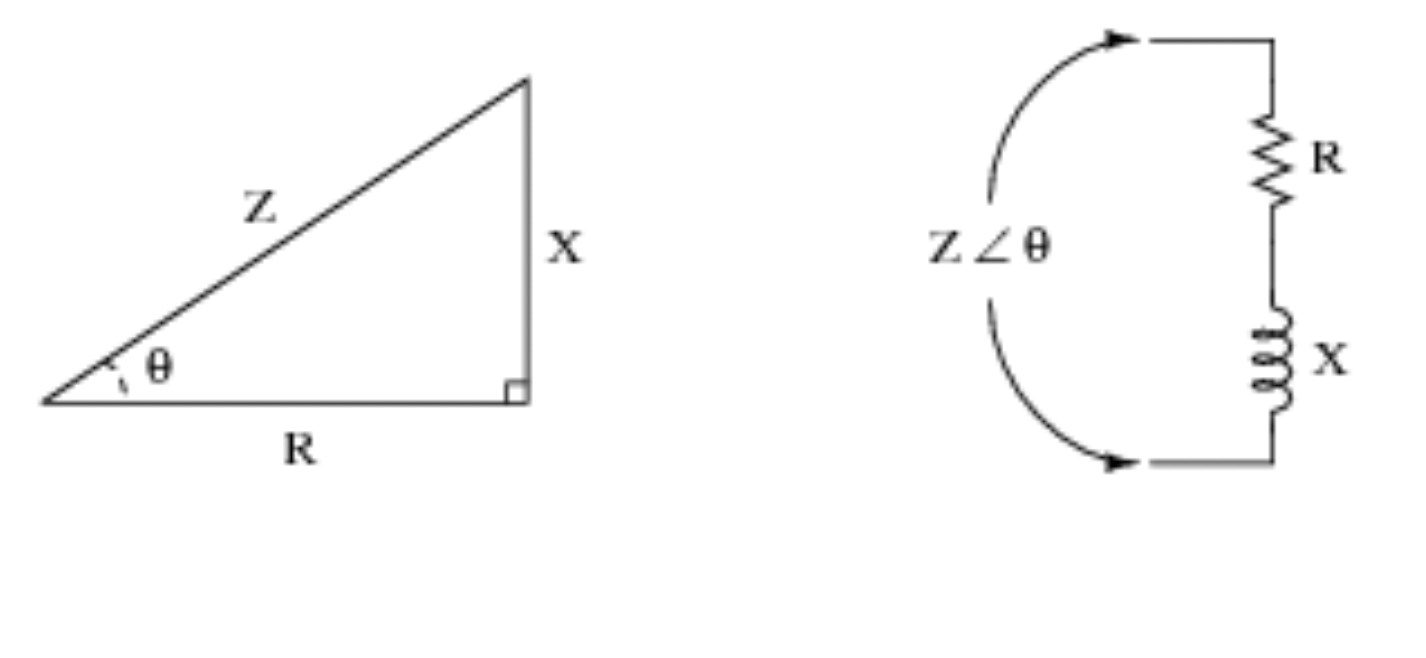
4) Seysmologiya
Seysmologiya zəlzələləri, eləcə də yer üzündə və ətrafında hərəkət edən seysmik dalğaları öyrənir. Triqonometriya seysmik dalğanın keçdiyi şaquli və üfüqi məsafənin hesablanmasını asanlaşdırmaq üçün daxil olur.

5) Torpaq tədqiqatı (inşaat mühəndisliyi)
Yerüstü tədqiqat uzun müddətdir mövcud olan bir peşədir, ən azı qeyd olunan tarix göstərir. Bu, yerin səthlərini geniş miqyasda dəqiq ölçmək işi olan bir sörveyer tərəfindən edilir. İndiyə qədər triqonometriyanın istifadəsini təxmin etmiş ola bilərsiniz; Əsasən, triqonometriya sörveyörün landşaftdakı obyektlər arasında uzunluğu, sahələri və nisbi bucaqları hesablamağa ehtiyacı olduqda gəlir.
Aşağıdakı nümunə əvvəllər izah edilənlərin yaxşı vizual nümayişidir. Tədqiqatçı dağın zirvəsindən və ya seçdiyi hər hansı başqa yerdən öz məsafəsini hesablamaq üçün triqonometrik fraksiyalardan istifadə edir.

Məqalə müəllifi
Parmis Kazemi
Parmis, yeni şeylər yazmaq və yaratmaq həvəsi olan bir məzmun yaradıcısıdır. Texnika ilə də çox maraqlanır və yeni şeylər öyrənməyi sevir.
Triqonometriya Kalkulyatoru Azərbaycan
Yayımlandı: Fri Oct 29 2021
Riyazi hesablayıcılar kateqoriyasında
Öz saytınıza Triqonometriya Kalkulyatoru əlavə edin