Matematické Kalkulačky
Kalkulačka Trigonometrie
Jednoducho vypočítajte trigonometrické hodnoty Sin, Cos, Tan, Cot, Sec a Csc pomocou našej bezplatnej online kalkulačky!
Kalkulačka trigonometrie
Obsah
| ◦Čo je to trigonometria? |
| ◦Aké sú primárne alebo základné goniometrické funkcie? |
| ◦Čo sú to recipročné goniometrické funkcie? |
| ◦Na čo sa používa trigonometria? |
| ◦Reálne aplikácie trigonometrie |
Čo je to trigonometria?
Trigonometria je časť matematiky, ktorá sa zaoberá stranami a uhlami v trojuholníku. Tento predmet zahŕňa aj príslušné funkcie používané na výpočet uhlov.
Aké sú primárne alebo základné goniometrické funkcie?
Nižšie uvidíte zoznam primárnych goniometrických funkcií, ktoré sa používajú hlavne pri využívaní trigonometrie.
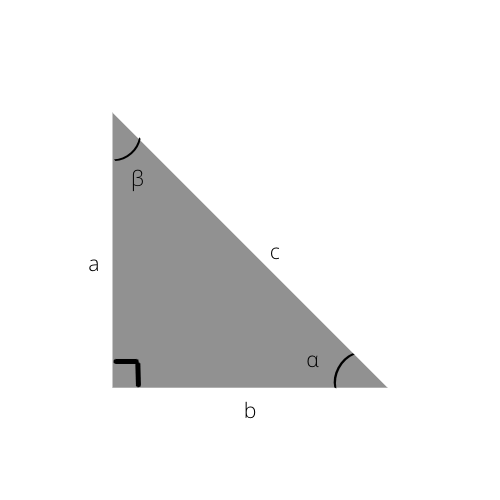
Príklad pravouhlého trojuholníka. Uhol "α" na tomto obrázku je uvedený v nasledujúcich vzorcoch.
1) Sínus uhla
Vzorec: sin α = opak / prepona
Pomer sínusu uhla v kontexte pravouhlého trojuholníka je dĺžka protiľahlej delená dĺžkou prepony.
2) Kosínus uhla
Vzorec: cos α = susedná / prepona
Kosínus uhla v kontexte pravouhlého trojuholníka sa vypočíta vydelením dĺžky susednej prepony dĺžkou prepony.
3) Tangenta uhla
Vzorec: tan α = sin α / cos α = protiľahlý / susedný
Tangent uhla v kontexte pravouhlého trojuholníka sa vypočíta vydelením sínusu kosínusom. Toto je možné nahradiť aj delením opaku susedným.
Pri používaní týchto funkcií pamätajte aj na trigonometrickú tabuľku.
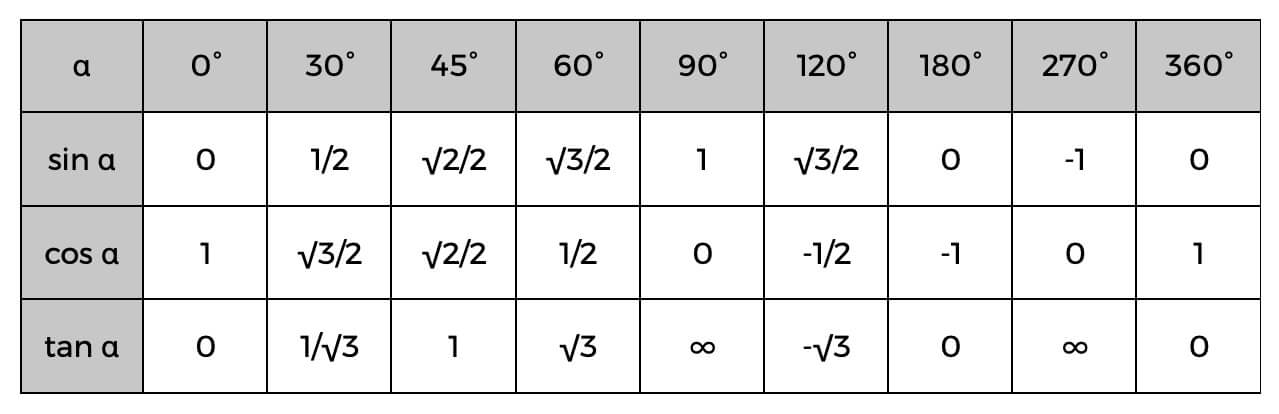
Trigonometrická tabuľka
Čo sú to recipročné goniometrické funkcie?
Okrem primárnych goniometrických funkcií existuje aj iná skupina funkcií, ktoré nie sú tak používané v porovnaní s prvou kategóriou. Patria sem sekanta (sec), kosekans (csc) a kotangens (cot).
Na čo sa používa trigonometria?
Trigonometria súvisí s trojuholníkmi, najmä pravouhlými trojuholníkmi. Takže, kdekoľvek uvidíte trojuholník mimo matematického sveta, stavte sa, že trigonometria je užitočná. Príkladom toho je použitie trigonometrických výpočtov v oblastiach ako architektúra, astronómia a chemické inžinierstvo.
Reálne aplikácie trigonometrie
Okrem zrejmého použitia trigonometrie, ktorá je v matematike, sa trigonometria používa aj v reálnych situáciách a oblastiach.
1) Architektúra a inžinierstvo
Nie je ďaleko k úvahám o využití goniometrických funkcií v architektúre. Tieto funkcie sa väčšinou používajú na výpočet dĺžky diagonálneho spojenia, ktoré spája dve čiary. Používa sa na výpočet diagonálnej dĺžky sklonu strechy pri navrhovaní šikmej strechy. Stačí poznať výšku a dĺžku strechy a môžete ísť!

2) Astronómia
Astronómia je dôležitým predmetom, ktorému staré kultúry väčšinou venovali pozornosť. Keď o tom hovoríme, pravdepodobne jedna z prvých vecí, ktoré prídu na myseľ, sú konštelácie a výpočet ich vzdialenosti od seba a iných objektov vo vesmíre, čo je jedno z najjednoduchších spôsobov použitia astronómie. Inými slovami, trigonometria sa dá použiť na výpočet vzdialenosti Slnka a Zeme od rôznych hviezd. Vzdialenosť hviezd je dôležitá pre výpočet ich faktorov vo svete astronómie.
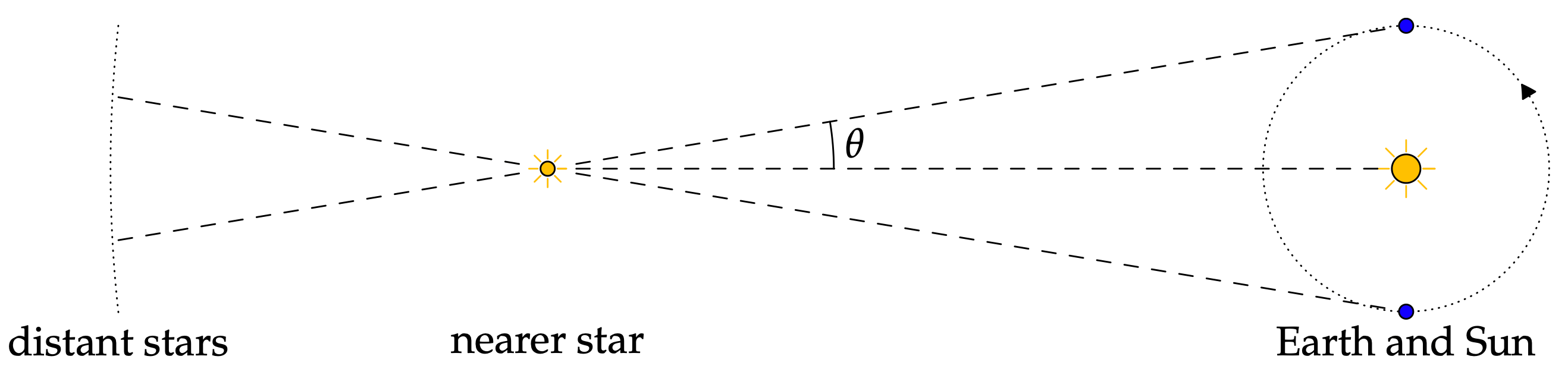
Ďalšie informácie o astronómii a jej vzťahu k trigonometrii nájdete v tomto článku:
3) Elektronika a elektrotechnika
Trigonometria sa používa na riešenie matematických úloh v elektronike a elektrotechnike, väčšinou pri navrhovaní modelu. Ďalším príkladom dôležitosti je pri vytváraní estetických doplnkov a uistení sa, že nenarúšajú funkciu modelu.
Pri práci s obvodmi však prídu veľmi vhod trigonometrické funkcie. Pozrite si nižšie uvedený vizuálny príklad pre ďalšiu demonštráciu a pre získanie predstavy o tom, ako sa trigonometria premieta do logiky obvodu.
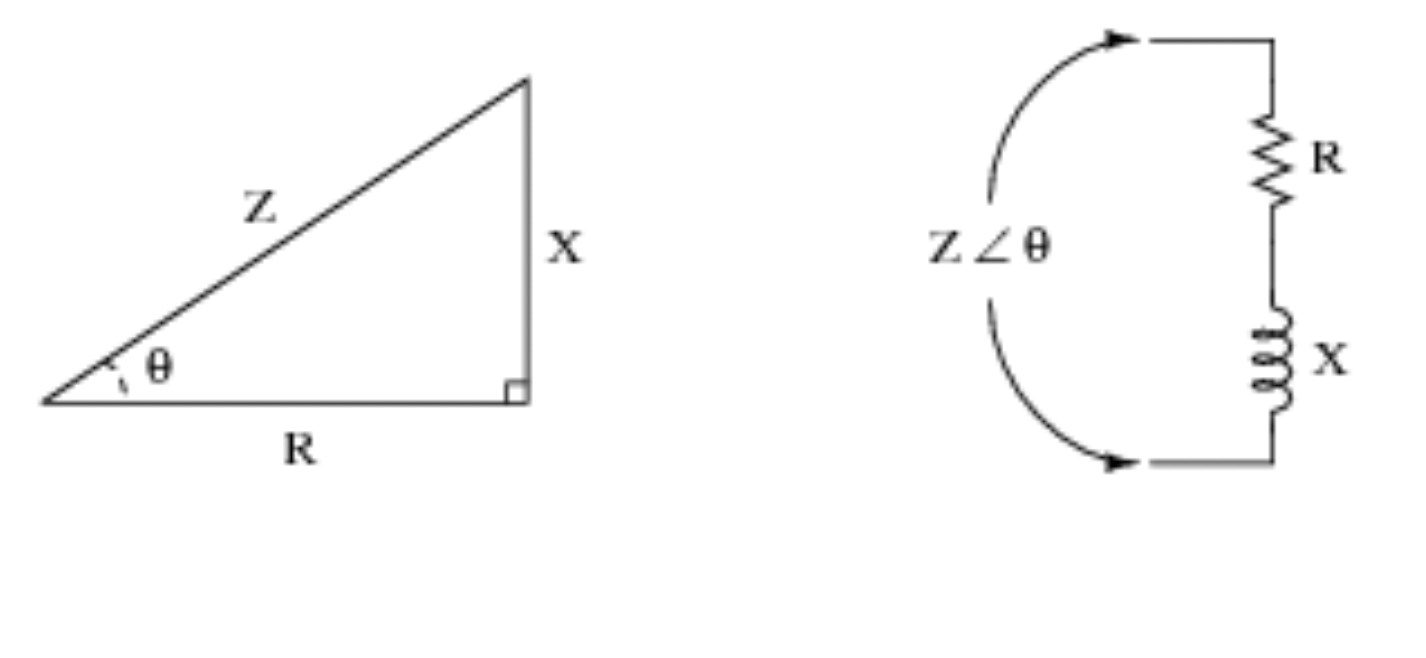
4) Seizmológia
Seizmológia je štúdium zemetrasení, ako aj seizmických vĺn, ktoré sa pohybujú cez zem a okolo nej. Trigonometria prichádza na uľahčenie výpočtu vertikálnej a horizontálnej vzdialenosti, ktorú prejde seizmická vlna.

5) Geodetické práce (stavebné inžinierstvo)
Geodézia je profesia, ktorá existuje už dlho, aspoň tak dlho, ako ukazuje zaznamenaná história. Robí to geodet, ktorý má za úlohu presne merať zemské povrchy vo veľkom meradle. Možno ste už uhádli použitie trigonometrie; v podstate trigonometria prichádza, keď geodet potrebuje vypočítať dĺžku, plochy a relatívne uhly medzi objektmi v krajine.
Nižšie uvedený príklad je dobrým vizuálnym demonštrantom toho, čo už bolo vysvetlené. Geodet používa trigonometrické zlomky na výpočet svojej vlastnej vzdialenosti od vrcholu hory alebo kdekoľvek inde, ktorú si vyberie.

Autor článku
Parmis Kazemi
Parmis je tvorca obsahu, ktorý má vášeň pre písanie a vytváranie nových vecí. Má tiež veľký záujem o techniku a rada sa učí nové veci.
Kalkulačka Trigonometrie Slovenčina
Publikovaný: Fri Oct 29 2021
V kategórii Matematické kalkulačky
Pridajte Kalkulačka Trigonometrie na svoj vlastný web