Matematické Kalkulačky
Kalkulačka Prepony Trojuholníka
Zistite preponu pre všetky druhy trojuholníkov jednoducho pomocou našej bezplatnej matematickej kalkulačky!
Trojuholníková prepona na dvoch stranách
Trojuholníková prepona na jednej strane a ploche
Obsah
Aká je prepona trojuholníka?
Prepona je najdlhšia strana trojuholníka. Je to aj strana opačná z pravého uhla (90°).
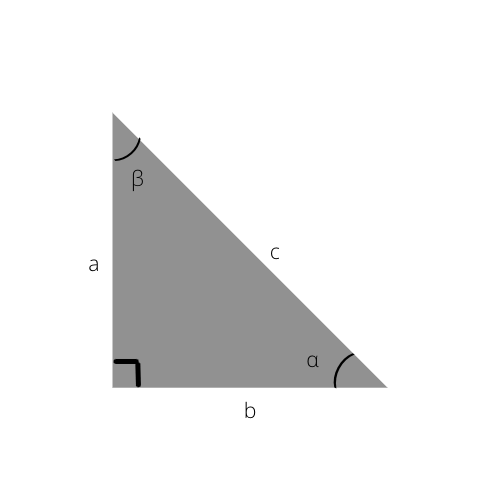
Prepona je c v tomto trojuholníku.
Môžete si tiež prečítať tento článok na Wikipédii:
Prečo je prepona najdlhšou stranou trojuholníka?
Po pozorovaní vyššie uvedeného obrázku a ostatných pravouhlých trojuholníkov si všimnete, že prepona je vždy najdlhšou stranou všetkých pravouhlých trojuholníkov. Je to jednoducho preto, že sa nachádza oproti najväčšiemu uhlu, 90°.
dá sa to dokázať aj matematicky pomocou Pytagorovej vety:
a² + b² = c²
a² > b² , a² > c²
a > b , a > c
Ako vidíte, výsledkom vyššie uvedenej operácie je, že "a" (prepona) je väčšia ako ostatné dve strany.
Ako vypočítať preponu trojuholníka?
Dá sa to urobiť 3 rôznymi spôsobmi v závislosti od daných informácií, ktoré môžu byť variáciou faktorov uvedených nižšie:
a: opačná strana
b: susedná strana
c: strana prepony
α: uhol medzi susednou a preponou
β: uhol medzi protipólom a preponou
1) Dve nohy pravouhlého trojuholníka
Formula: c = √(a² + b²) or c² = a² + b²
Tento vzorec je založený na Pytagorovej vete, ktorú možno jednoducho použiť odmocninou zo súčtu druhých mocnín susedných a opačných.
2) Uhol a jedna noha
Formula: c = a / sin(α) = b / sin(β)
Preponu môžete vypočítať aj pomocou sínusového zákona, ktorý je základom tohto vzorca.
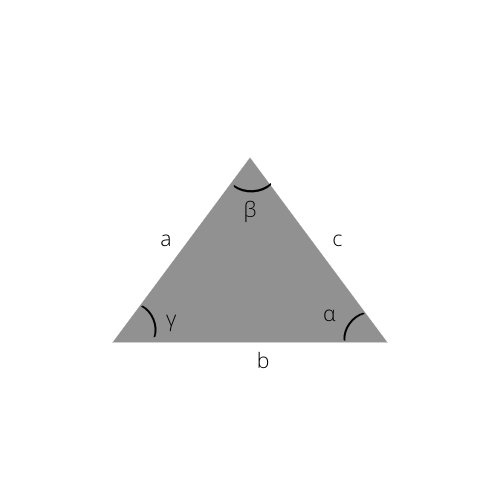
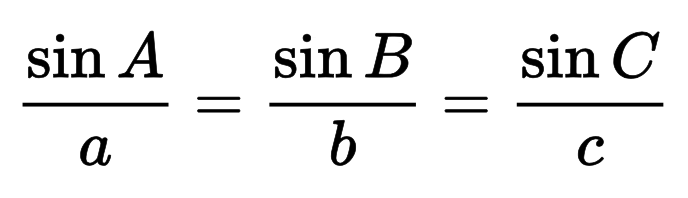
Všeobecný zákon sínusov
3) Plocha a jedna noha
Formula: c = √(a² + b²) = √(a² + (area _ 2 / a)²) = √((area _ 2 / b)² + b²)
Tento vzorec je založený na vzorci, ktorý používame na výpočet plochy trojuholníka (a \* b / 2). Oproti ostatným dvom to vyzerá komplikovanejšie, no má rovnakú logiku ako ostatné dva spôsoby výpočtu prepony.
Je dobré vedieť o goniometrických funkciách
Ak sa stále chcete dozvedieť viac o pravouhlom trojuholníku, pozrite si tieto trigonometrické funkcie.
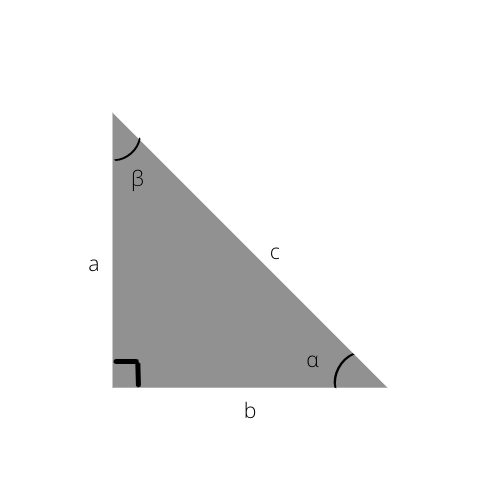
Keď to poznáte, môžete ľahko vypočítať strany pravouhlého trojuholníka alebo dokonca určiť uhly pomocou nižšie uvedenej trigonometrickej tabuľky.
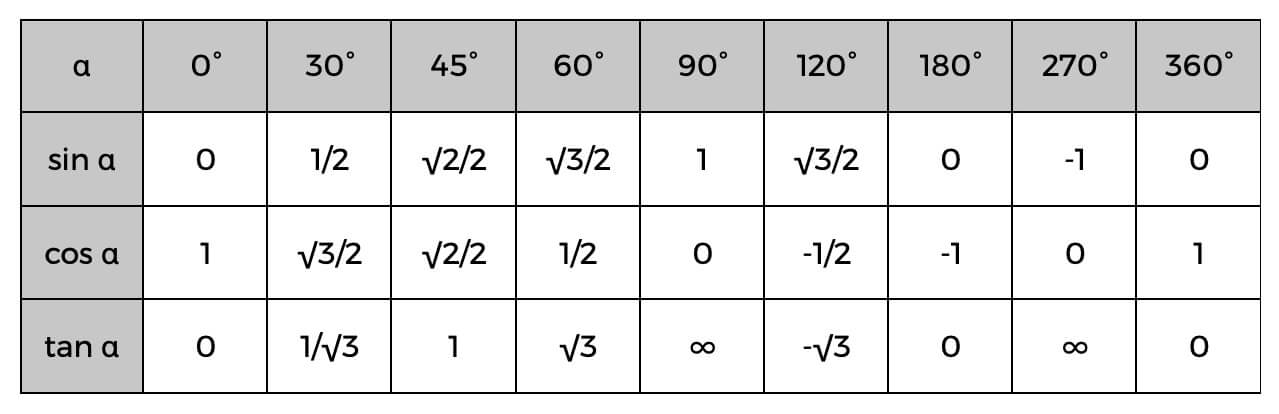
Príkladom toho môže byť, že už poznáte hodnotu prepony a priľahlého; môžete ľahko nájsť kosínus uhla, potom skontrolujte tabuľku vyššie, aby ste našli presný uhol alebo len odhad toho, čo by to mohlo byť. Ak je kosínus alfa (α) 0,5, potom vieme, že uhol je 60°.
Môžete si tiež prečítať tento článok na Wikipédii:
Klasifikácia trojuholníkov podľa strán
1) Rovnostranný
Tento trojuholník má tri rovnaké strany. Výsledkom je, že všetky uhly sú 60°.
Vizuálny príklad:

Rovnostranný trojuholník
2) Rovnoramenné
V tomto trojuholníku sú rovnaké iba dve strany.
Vizuálny príklad:

Rovnoramenný trojuholník
3) Scalene
Žiadna zo strán v tomto trojuholníku nie je rovnaká.
Vizuálny príklad

Rôznostranný trojuholník
Klasifikácia trojuholníkov na základe uhlov
1) Akútne
Všetky tri uhly v tomto trojuholníku sú menšie ako 90°.
Vizuálny príklad:

Akútny trojuholník
2) Správne
Tento trojuholník má iba jeden uhol 90°, čo má za následok, že ostatné dva sú menšie ako 90°.
prečo?
α + β + γ = 180° & α = 90° → β + γ = 90° → β , γ < 90°
Vizuálny príklad:

Správny trojuholník
3) Tupý
Tento trojuholník má jeden uhol väčší ako 90°.
Vizuálny príklad:

Tupý trojuholník
Zábavné fakty o trojuholníkoch
Fakt 1:
Ak je nakreslená vnútorná výška trojuholníka, dostaneme dva pravouhlé trojuholníky v pôvodnom trojuholníku.
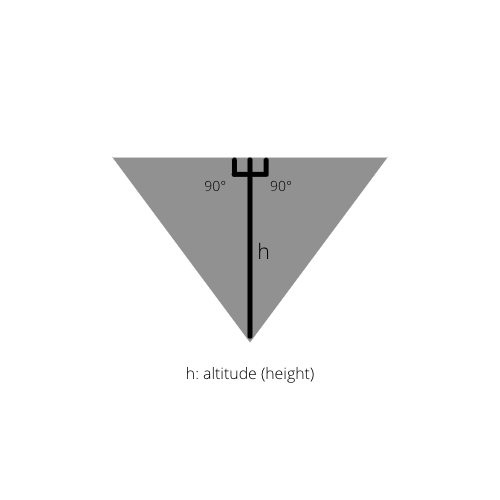
Fakt 2:
Ako vieme, obsah akéhokoľvek trojuholníka (A) je polovica výšky vynásobená základňou (A = 1/2 _ b _ h). Tento vzorec môže byť napísaný špeciálnym spôsobom pre rovnoramenný pravouhlý trojuholník, pretože jeho plocha je polovica plochy štvorca.
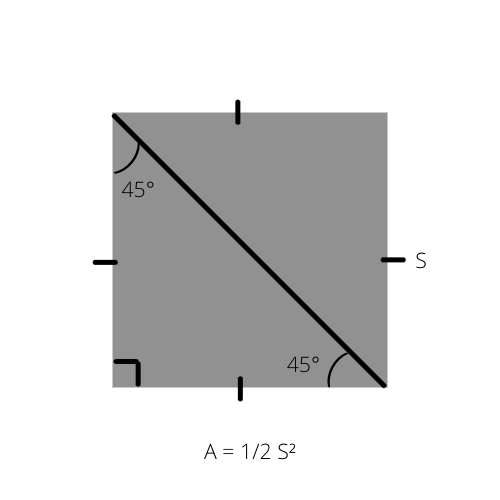
A je plocha trojuholníka a S je strana štvorca.
Fakt 3:
Súčet všetkých troch uhlov trojuholníka je vždy 180°. To platí o všetkých trojuholníkoch.
Autor článku
Parmis Kazemi
Parmis je tvorca obsahu, ktorý má vášeň pre písanie a vytváranie nových vecí. Má tiež veľký záujem o techniku a rada sa učí nové veci.
Kalkulačka Prepony Trojuholníka Slovenčina
Publikovaný: Wed Oct 27 2021
V kategórii Matematické kalkulačky
Pridajte Kalkulačka Prepony Trojuholníka na svoj vlastný web
Kalkulačka Prepony Trojuholníka v iných jazykoch
Калкулатор За Хипотенуза На ТриъгълникKalkulator Hipotenuze TrokutaTrikampio Hipotenuzės SkaičiuotuvasCalcolatrice Triangolo IpotenusaTriangle Hypotenuse CalculatorKalkulator Hipotenus SegitigaTriangel Hypotenusa RäknareKolmion Hypotenuusan LaskinTrekanthypotenuskalkulatorLommeregner For Trekant Hypotenus