Matematični Kalkulatorji
Kalkulator Hipotenuze Trikotnika
Z našim brezplačnim matematičnim kalkulatorjem enostavno ugotovite hipotenuzo za vse vrste trikotnikov!
Hipotenuza trikotnika po dveh straneh
Hipotenuza trikotnika po eni strani in površini
Kazalo
Kakšna je hipotenuza trikotnika?
Hipotenuza je najdaljša stranica trikotnika. Je tudi stran, nasprotna od pravega kota (90°).
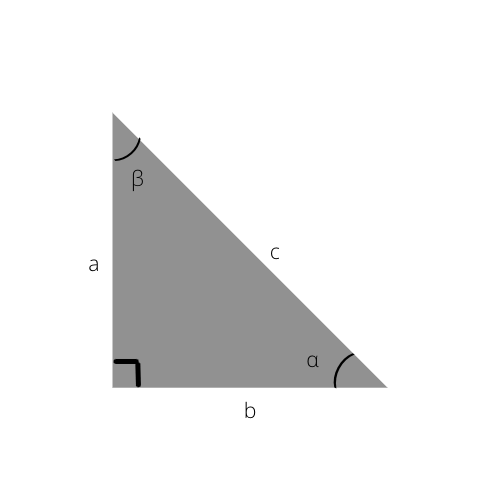
Hipotenuza je v tem trikotniku c.
Lahko si ogledate tudi ta članek na Wikipediji:
Zakaj je hipotenuza najdaljša stranica trikotnika?
Po opazovanju zgornje slike in drugih pravokotnih trikotnikov boste opazili, da je hipotenuza vedno najdaljša stranica vseh pravokotnih trikotnikov. To je preprosto zato, ker se nahaja nasproti največjega kota, kota 90°.
to je mogoče dokazati tudi matematično z uporabo Pitagorovega izreka:
a² + b² = c²
a² > b² , a² > c²
a > b , a > c
Kot vidite, je rezultat zgornje operacije, da je "a" (hipotenuza) večja od drugih dveh strani.
Kako izračunati hipotenuzo trikotnika?
To je mogoče storiti na 3 različne načine, odvisno od danih informacij, ki so lahko različica spodaj navedenih dejavnikov:
a: nasprotna stran
b: sosednja stran
c: hipotenuzna stran
α: kot med sosednjo in hipotenuzo
β: kot med nasprotjem in hipotenuzo
1) Dva pravokotna trikotna kraka
Formula: c = √(a² + b²) or c² = a² + b²
Ta formula temelji na Pitagorejevem izreku, ki ga je mogoče preprosto uporabiti tako, da vzamemo kvadratni koren iz vsote kvadratov sosednjega in nasprotnega.
2) Kot in ena noga
Formula: c = a / sin(α) = b / sin(β)
Hipotenuzo lahko izračunate tudi z uporabo zakona sinusov, ki je osnova te formule.
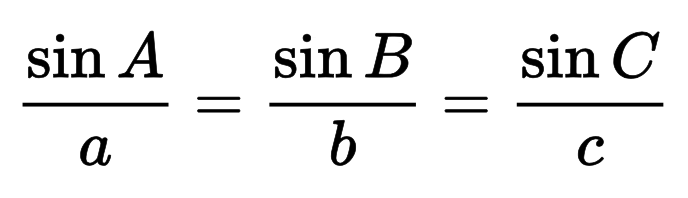
Splošni zakon sinusov
3) Območje in ena noga
Formula: c = √(a² + b²) = √(a² + (area _ 2 / a)²) = √((area _ 2 / b)² + b²)
Ta formula temelji na formuli, ki jo uporabljamo za izračun površine trikotnika (a \* b / 2). V primerjavi z ostalima dvema je videti bolj zapleteno, vendar sledi isti logiki kot druga dva načina izračunavanja hipotenuz.
Dobro je vedeti o trigonometričnih funkcijah
Če še vedno želite izvedeti več o desnem trikotniku, si oglejte te trigonometrične funkcije.
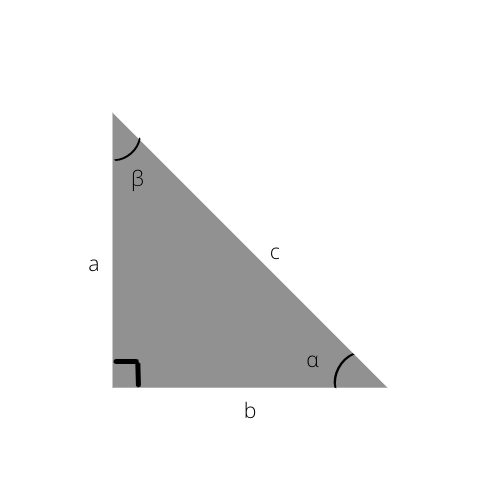
Če jih poznate, lahko enostavno izračunate stranice pravokotnega trikotnika ali celo določite kote s spodnjo trigonometrično tabelo.
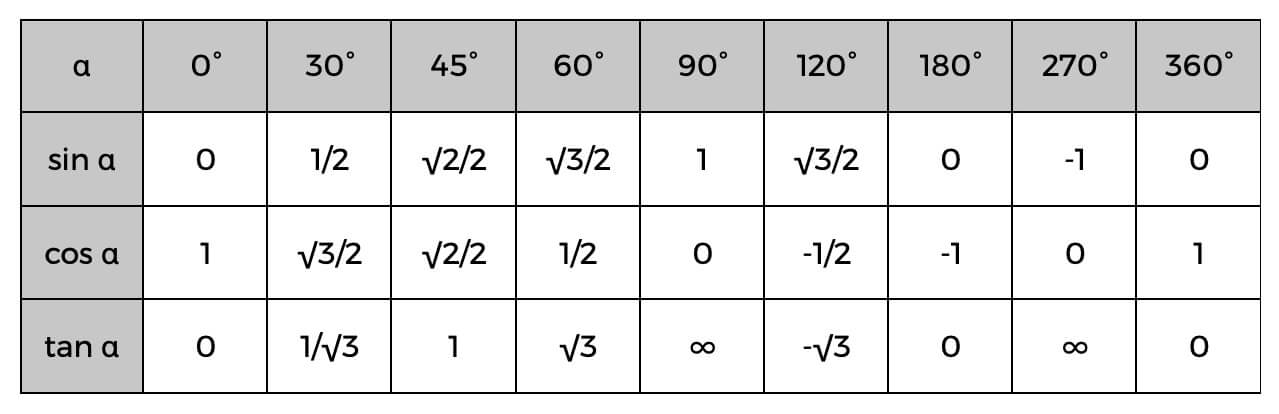
Primer tega je lahko, da že poznate vrednost hipotenuze in sosednje; zlahka najdete kosinus kota, nato preverite zgornjo tabelo, da najdete natančen kot ali samo oceno, kaj bi lahko bil. Če je kosinus alfa (α) 0,5, potem vemo, da je kot 60°.
Lahko si ogledate tudi ta članek na Wikipediji:
Razvrstitev trikotnikov na podlagi stranic
1) Enakostranični
Ta trikotnik ima tri enake stranice. Tako so vsi koti 60°.
Vizualni primer:

Enakostranični trikotnik
2) Enakokraki
V tem trikotniku sta samo dve strani enaki.
Vizualni primer:

Enakokraki trikotnik
3) Scale
Nobena od stranic v tem trikotniku ni enaka.
Vizualni primer

Skalen trikotnik
Razvrstitev trikotnikov glede na kote
1) Akutna
Vsi trije koti v tem trikotniku so manjši od 90°.
Vizualni primer:

Ostri trikotnik
2) Prav
Ta trikotnik ima samo en kot 90°, pri čemer sta druga dva manjša od 90°.
Zakaj?
α + β + γ = 180° & α = 90° → β + γ = 90° → β , γ < 90°
Vizualni primer:

Pravokotni trikotnik
3) Topo
Ta trikotnik ima en kot večji od 90°.
Vizualni primer:

Tupi trikotnik
Zabavna dejstva o trikotnikih
1. dejstvo:
Če narišemo notranjo višino trikotnika, dobimo v prvotnem trikotniku dva pravokotna trikotnika.
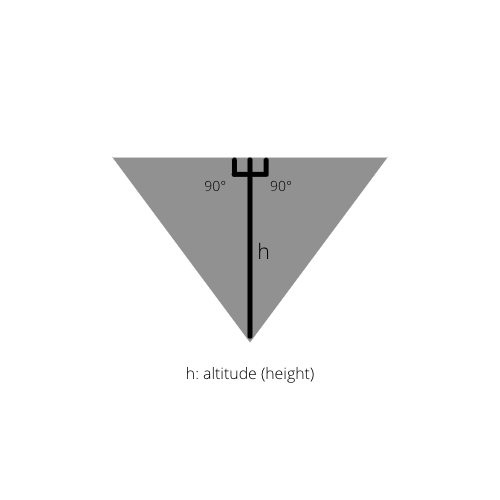
2. dejstvo:
Kot vemo, je površina katerega koli trikotnika (A) polovica višine, pomnožena z osnovo (A = 1/2 _ b _ h). To formulo lahko zapišemo na poseben način za enakokraki pravokotnik, saj je njegova površina polovica površine kvadrata.
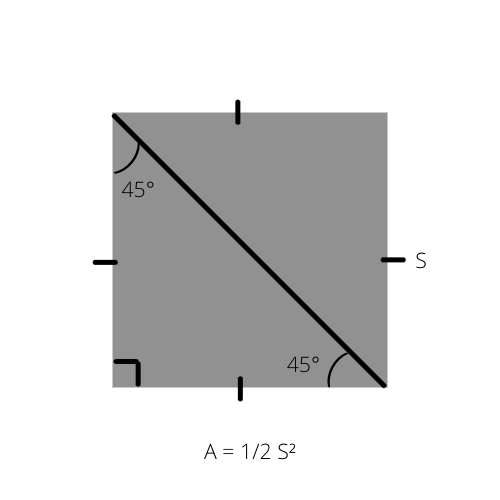
A je površina trikotnika, S pa stran kvadrata.
3. dejstvo:
Vsota vseh treh kotov trikotnika je vedno 180°. To velja za vse trikotnike.
Avtor članka
Parmis Kazemi
Parmis je ustvarjalec vsebin, ki ima strast do pisanja in ustvarjanja novih stvari. Zelo jo zanima tudi tehnika in se rada uči novih stvari.
Kalkulator Hipotenuze Trikotnika Slovenski
Objavljeno: Wed Oct 27 2021
V kategoriji Matematični kalkulatorji
Dodajte Kalkulator Hipotenuze Trikotnika na svoje spletno mesto