Kalkulator Matematika
Kalkulator Hipotenusa Segitiga
Cari tahu sisi miring untuk semua jenis segitiga dengan mudah dengan kalkulator matematika gratis kami!
Sisi miring segitiga dengan dua sisi
Sisi miring segitiga dengan satu sisi dan luas
Daftar Isi
Apa hipotenusa segitiga?
Hipotenusa adalah sisi terpanjang dari sebuah segitiga. Itu juga sisi yang berlawanan dari sudut kanan (90°).
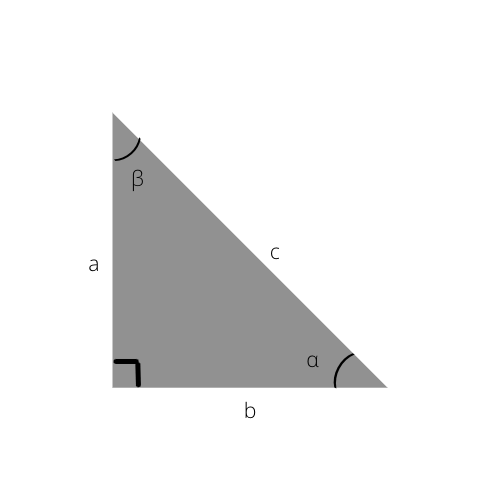
Hipotenusanya adalah c dalam segitiga ini.
Anda juga dapat melihat artikel Wikipedia ini:
Mengapa sisi miring segitiga tersebut merupakan sisi terpanjang?
Setelah mengamati gambar di atas, dan segitiga siku-siku lainnya, Anda akan melihat bahwa sisi miring selalu merupakan sisi terpanjang dari semua segitiga siku-siku. Ini hanya karena terletak di seberang sudut terbesar, sudut 90°.
ini juga dapat dibuktikan secara matematis dengan menggunakan Teorema Pythagoras:
a² + b² = c²
a² > b² , a² > c²
a > b , a > c
Seperti yang Anda lihat, hasil dari operasi di atas adalah bahwa "a" (sisi miring) lebih besar dari dua sisi lainnya.
Bagaimana cara menghitung hipotenusa segitiga?
Ini dapat dilakukan dengan 3 cara berbeda, tergantung pada informasi yang diberikan yang dapat menjadi variasi dari faktor-faktor yang tercantum di bawah ini:
a: sisi yang berlawanan
b: sisi yang berdekatan
c: sisi miring
: sudut antara sisi yang berdekatan dan sisi miring
: sudut antara berlawanan dan sisi miring
1) Dua kaki segitiga siku-siku
Formula: c = √(a² + b²) or c² = a² + b²
Rumus ini didasarkan pada teorema Pythagoras yang dapat digunakan secara sederhana dengan mengambil akar kuadrat dari jumlah kuadrat dari yang berdekatan dan yang berlawanan.
2) Sudut dan satu kaki
Formula: c = a / sin(α) = b / sin(β)
Anda juga dapat menghitung sisi miring dengan menggunakan hukum sinus, yang merupakan dasar dari rumus ini.
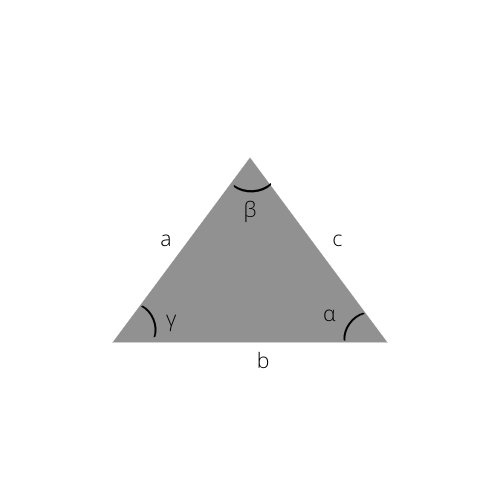
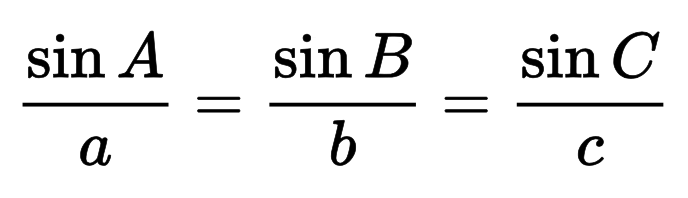
Hukum umum sinus
3) Area dan satu kaki
Formula: c = √(a² + b²) = √(a² + (area _ 2 / a)²) = √((area _ 2 / b)² + b²)
Rumus ini didasarkan pada rumus yang kita gunakan untuk menghitung luas segitiga (a \* b / 2). Dibandingkan dengan dua lainnya, ini terlihat lebih rumit, namun mengikuti logika yang sama dengan dua cara menghitung sisi miring lainnya.
Baik untuk mengetahui tentang fungsi trigonometri
Jika Anda masih ingin mengetahui lebih banyak tentang segitiga siku-siku, lihat fungsi Trigonometri ini.
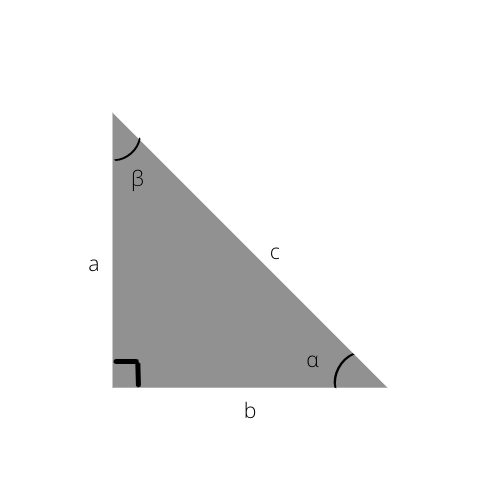
Mengetahui hal ini, Anda dapat dengan mudah menghitung sisi segitiga siku-siku, atau bahkan menentukan sudut menggunakan tabel Trigonometri di bawah ini.
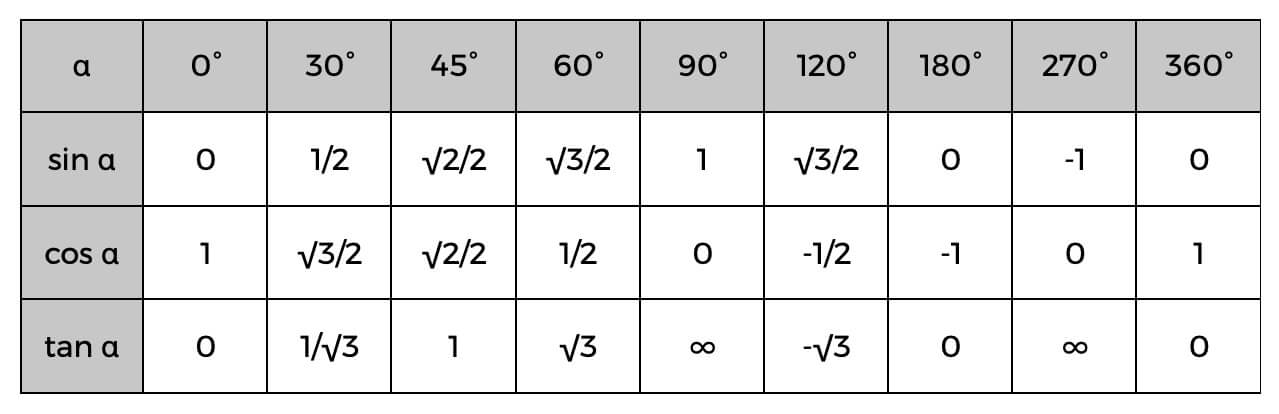
Contohnya adalah Anda sudah mengetahui nilai sisi miring dan tetangganya; Anda dapat dengan mudah menemukan kosinus dari sudut, kemudian periksa tabel di atas untuk menemukan sudut yang tepat atau hanya perkiraan dari apa itu. Jika kosinus alfa (α) adalah 0,5, maka kita tahu bahwa sudutnya adalah 60°.
Anda juga dapat melihat artikel Wikipedia ini:
Klasifikasi segitiga berdasarkan sisinya
1) Sama sisi
Segitiga ini memiliki tiga sisi yang sama panjang. Ini menghasilkan semua sudut menjadi 60 °.
Contoh visual:

Segitiga sama sisi
2) Sama kaki
Pada segitiga ini hanya dua sisi yang sama besar.
Contoh visual:

Segitiga sama kaki
3) Skala
Tidak ada sisi yang sama dalam segitiga ini.
Contoh visual

segitiga skalen
Klasifikasi segitiga berdasarkan sudutnya
1) Akut
Ketiga sudut dalam segitiga ini lebih kecil dari 90°.
Contoh visual:

Segitiga lancip
2) Benar
Segitiga ini hanya memiliki satu sudut 90°, sehingga dua sudut lainnya kurang dari 90°.
Mengapa?
α + β + γ = 180° & α = 90° → β + γ = 90° → β , γ < 90°
Contoh visual:

Segitiga siku-siku
3) Tumpul
Segitiga ini memiliki salah satu sudut yang besarnya lebih dari 90°.
Contoh visual:

segitiga tumpul
Fakta menarik tentang segitiga
Fakta 1:
Jika ketinggian bagian dalam segitiga digambar, kita mendapatkan dua segitiga siku-siku dalam segitiga aslinya.
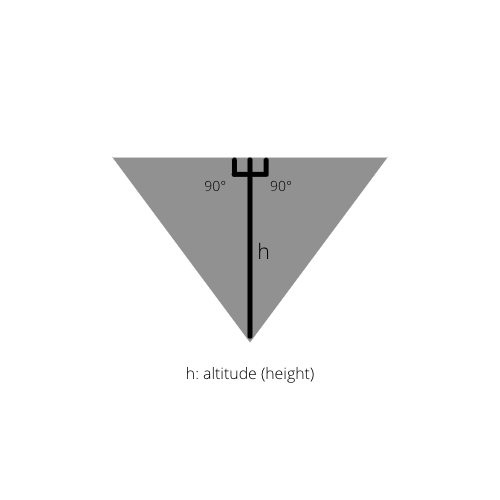
Fakta 2:
Seperti yang kita ketahui, luas segitiga (A) adalah setengah dari tinggi dikalikan alas (A = 1/2 _ b _ h). Rumus ini dapat ditulis dengan cara khusus untuk segitiga siku-siku sama kaki karena luasnya adalah setengah dari luas persegi.
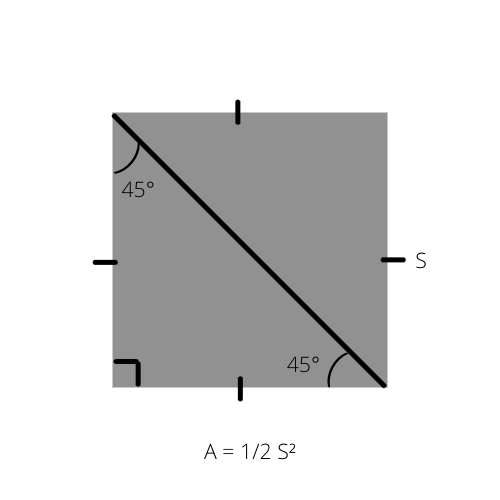
A adalah luas segitiga, dan S adalah sisi persegi.
Fakta 3:
Jumlah ketiga sudut segitiga selalu 180°. Ini berlaku untuk semua segitiga.
Penulis artikel
Parmis Kazemi
Parmis adalah seorang content creator yang memiliki passion untuk menulis dan menciptakan hal-hal baru. Dia juga sangat tertarik dengan teknologi dan senang mempelajari hal-hal baru.
Kalkulator Hipotenusa Segitiga Indonesia
Diterbitkan: Wed Oct 27 2021
Dalam kategori Kalkulator matematika
Tambahkan Kalkulator Hipotenusa Segitiga ke situs web Anda sendiri
Kalkulator Hipotenusa Segitiga dalam bahasa lain
Calculator De Ipotenuză TriunghiКалькулятар Гіпатэнузы ТрохкутнікаKalkulačka Prepony TrojuholníkaКалкулатор За Хипотенуза На ТриъгълникKalkulator Hipotenuze TrokutaTrikampio Hipotenuzės SkaičiuotuvasCalcolatrice Triangolo IpotenusaTriangle Hypotenuse CalculatorKalkulator Hipotenus SegitigaTriangel Hypotenusa Räknare