Matematiske Regnemaskiner
Lommeregner For Trekant Hypotenus
Find nemt ud af hypotenusen for alle slags trekanter med vores gratis matematikberegner!
Trekant hypotenusen ved to sider
Trekant hypotenusen ved den ene side og areal
Indholdsfortegnelse
Hvad er hypotenusen af en trekant?
Hypotenusen er den længste side af en trekant. Det er også siden modsat fra den rette vinkel (90°).
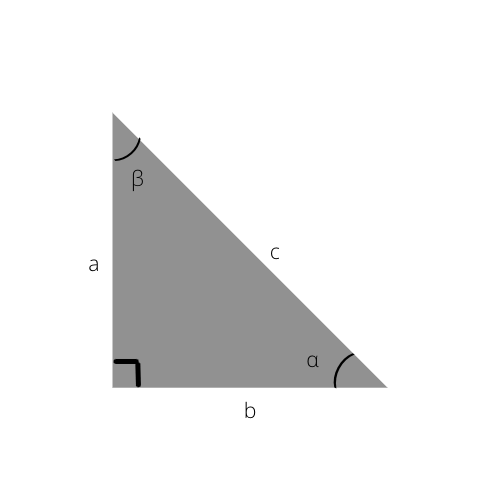
Hypotenusen er c i denne trekant.
Du kan også tjekke denne Wikipedia-artikel:
Hvorfor er hypotenusen den længste side af trekanten?
Efter at have observeret billedet ovenfor, og andre retvinklede trekanter, vil du bemærke, at hypotenusen altid er den længste side af alle de retvinklede trekanter. Dette er simpelthen fordi det er placeret modsat den største vinkel, 90°-vinklen.
dette kan også bevises matematisk ved at bruge Pythagoras sætning:
a² + b² = c²
a² > b² , a² > c²
a > b , a > c
Som du kan se, er resultatet af operationen ovenfor, at "a" (hypotenusen) er større end de to andre sider.
Hvordan beregner man hypotenusen af en trekant?
Dette kan gøres på 3 forskellige måder, afhængigt af den givne information, der kan være en variation af faktorerne anført nedenfor:
a: modsatte side
b: tilstødende side
c: hypotenussiden
α: vinkel mellem den tilstødende og hypotenusen
β: vinkel mellem modsat og hypotenusen
1) To retvinklede trekantede ben
Formula: c = √(a² + b²) or c² = a² + b²
Denne formel er baseret på Pythagoras sætning, som ganske enkelt kan bruges ved at tage en kvadratrod af summen af kvadraterne af den tilstødende og modsatte.
2) Vinkel og et ben
Formula: c = a / sin(α) = b / sin(β)
Du kan også beregne hypotenusen ved at bruge sinusloven, som er grundlaget for denne formel.
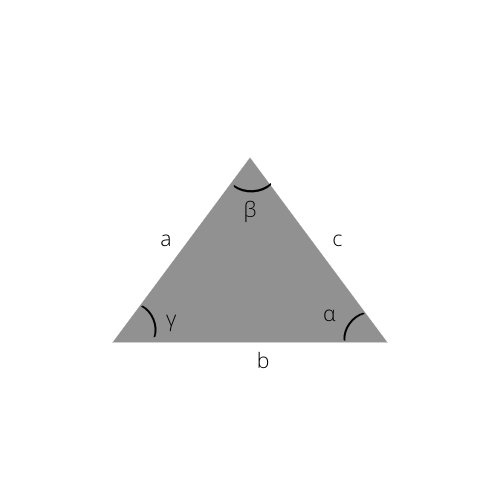
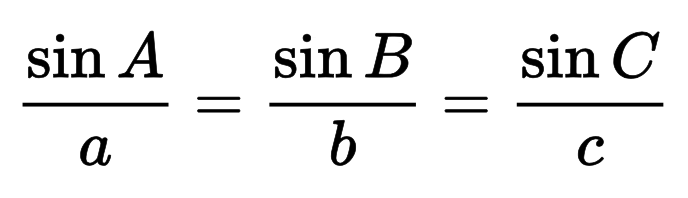
Den almindelige sinuslov
3) Område og et ben
Formula: c = √(a² + b²) = √(a² + (area _ 2 / a)²) = √((area _ 2 / b)² + b²)
Denne formel er baseret på den formel, vi bruger til at beregne arealet af en trekant (a \* b / 2). Sammenlignet med de to andre ser det mere kompliceret ud, men det følger samme logik som de to andre måder at beregne hypotenuser på.
Godt at vide om trigonometriske funktioner
Hvis du stadig er ivrig efter at vide mere om den rigtige trekant, så tjek disse trigonometriske funktioner.
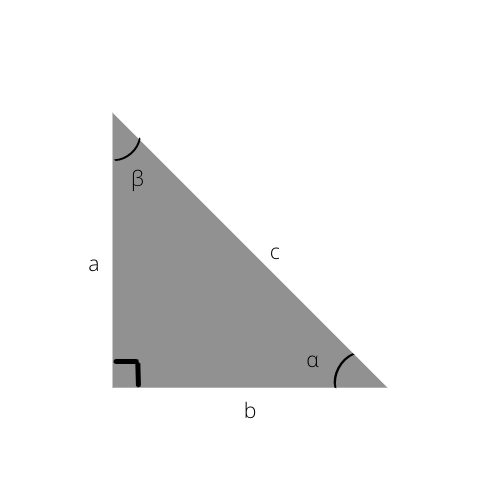
Når du kender disse, kan du nemt beregne siderne af den retvinklede trekant eller endda bestemme vinklerne ved hjælp af den trigonometriske tabel nedenfor.
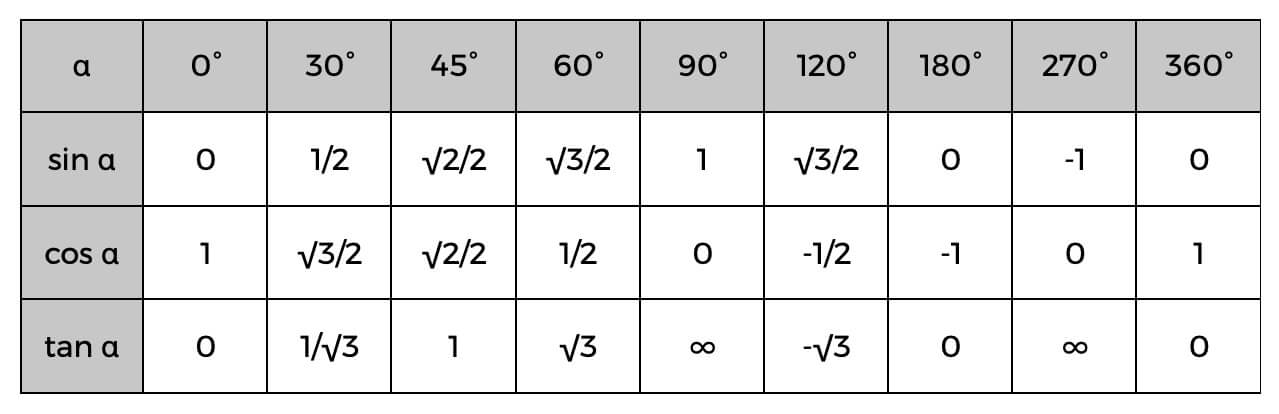
Et eksempel på dette kan være, at du allerede kender værdien af hypotenusen og den tilstødende; du kan nemt finde cosinus af vinklen, og tjek derefter tabellen ovenfor for at finde den nøjagtige vinkel eller blot et skøn over, hvad det kunne være. Hvis cosinus for alfa (α) er 0,5, så ved vi, at vinklen er 60°.
Du kan også tjekke denne Wikipedia-artikel:
Klassificering af trekanter baseret på siderne
1) Ligesidet
Denne trekant har tre lige sider. Dette resulterer i, at alle vinklerne er 60°.
Visuelt eksempel:

Ligesidet trekant
2) Ligebenet
I denne trekant er kun to sider ens.
Visuelt eksempel:

Ligebenet trekant
3) Skala
Ingen af siderne er lige store i denne trekant.
Visuelt eksempel

Skala trekant
Klassificering af trekanter baseret på vinklerne
1) Akut
Alle tre vinkler i denne trekant er mindre end 90°.
Visuelt eksempel:

Akut trekant
2) rigtigt
Denne trekant har kun én vinkel på 90°, hvilket resulterer i, at de to andre er mindre end 90°.
Hvorfor?
α + β + γ = 180° & α = 90° → β + γ = 90° → β , γ < 90°
Visuelt eksempel:

retvinklet trekant
3) Stump
Denne trekant har en vinkel, der er større end 90°.
Visuelt eksempel:

Stump trekant
Sjove fakta om trekanter
Fakta 1:
Hvis trekantens indre højde er tegnet, får vi to rette trekanter i den oprindelige trekant.
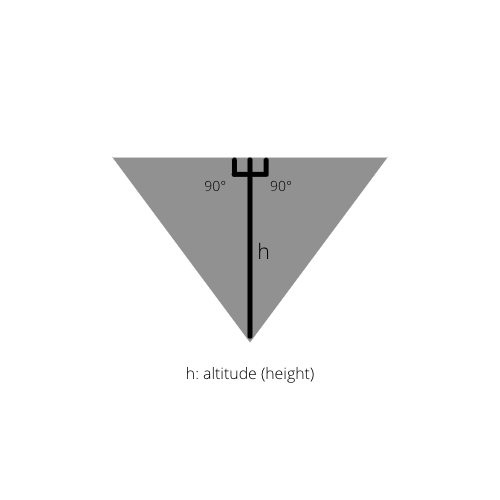
Fakta 2:
Som vi ved, er arealet af enhver trekant (A) halvdelen af højden ganget med grundfladen (A = 1/2 _ b _ h). Denne formel kan skrives på en speciel måde for den ligebenede retvinklede trekant, da dens areal er halvdelen af et kvadrats areal.
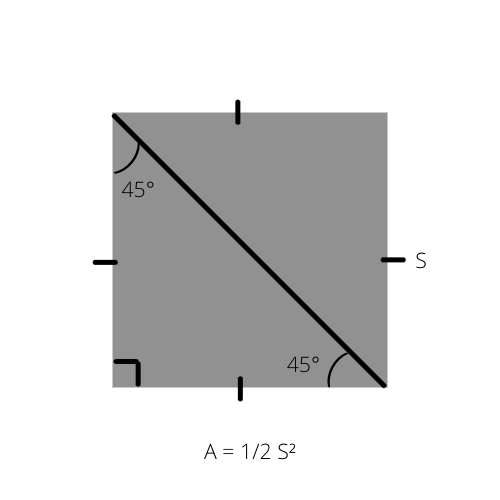
A er arealet af trekanten, og S siden af kvadratet.
Fakta 3:
Summen af alle tre vinkler i en trekant er altid 180°. Dette gælder for alle trekanter.
Artikelforfatter
Parmis Kazemi
Parmis er en indholdsskaber, der har en passion for at skrive og skabe nye ting. Hun er også meget interesseret i teknologi og nyder at lære nye ting.
Lommeregner For Trekant Hypotenus Dansk
Udgivet: Wed Oct 27 2021
I kategori Matematiske regnemaskiner
Føj Lommeregner For Trekant Hypotenus til dit eget websted