गणितीय कैलकुलेटर
त्रिभुज कर्ण कैलकुलेटर
हमारे मुफ़्त गणित कैलकुलेटर के साथ आसानी से सभी प्रकार के त्रिभुजों के लिए कर्ण का पता लगाएं!
दो पक्षों से त्रिभुज कर्ण
त्रिभुज कर्ण एक तरफ और क्षेत्रफल
विषयसूची
त्रिभुज का कर्ण क्या है?
कर्ण त्रिभुज की सबसे लंबी भुजा होती है। यह समकोण (90°) से विपरीत भुजा भी है।
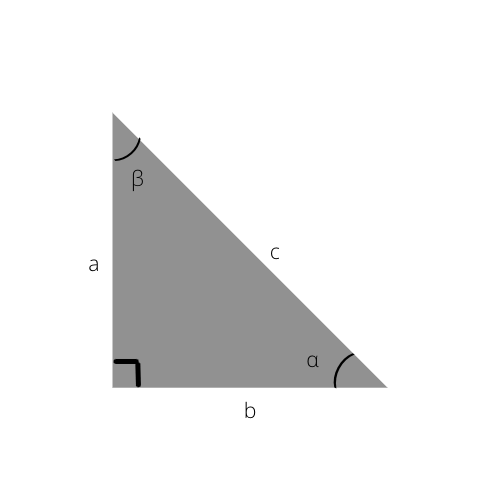
इस त्रिभुज में कर्ण c है।
आप इस विकिपीडिया लेख को भी देख सकते हैं:
कर्ण त्रिभुज की सबसे लंबी भुजा क्यों है?
ऊपर दिए गए चित्र और अन्य समकोण त्रिभुजों को देखने के बाद, आप देखेंगे कि कर्ण हमेशा सभी समकोण त्रिभुजों की सबसे लंबी भुजा होती है। यह केवल इसलिए है क्योंकि यह सबसे बड़े कोण, 90° कोण के विपरीत स्थित है।
यह पाइथागोरस प्रमेय का उपयोग करके गणितीय रूप से भी सिद्ध किया जा सकता है:
a² + b² = c²
a² > b² , a² > c²
a > b , a > c
जैसा कि आप देख रहे हैं, उपरोक्त ऑपरेशन का नतीजा यह है कि "ए" (कर्ण) अन्य दो पक्षों से बड़ा है।
त्रिभुज के कर्ण की गणना कैसे करें?
यह दी गई जानकारी के आधार पर 3 अलग-अलग तरीकों से किया जा सकता है, जो नीचे सूचीबद्ध कारकों की भिन्नता हो सकती है:
ए: विपरीत पक्ष
बी: आसन्न पक्ष
सी: कर्ण पक्ष
α: आसन्न और कर्ण के बीच का कोण
β: विपरीत और कर्ण के बीच का कोण
1) दो समकोण त्रिभुज पैर
Formula: c = √(a² + b²) or c² = a² + b²
यह सूत्र पाइथागोरस प्रमेय पर आधारित है जिसका उपयोग आसन्न और विपरीत के वर्गों के योग का वर्गमूल लेकर किया जा सकता है।
2) कोण और एक पैर
Formula: c = a / sin(α) = b / sin(β)
आप ज्या के नियम का उपयोग करके भी कर्ण की गणना कर सकते हैं, जो इस सूत्र का आधार है।
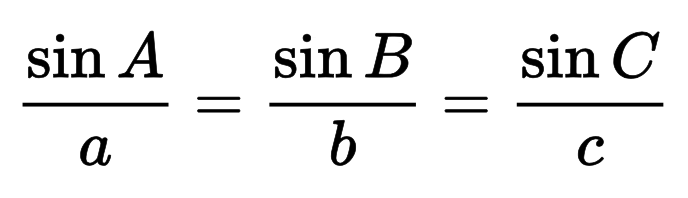
ज्या का सामान्य नियम
3) क्षेत्र और एक पैर
Formula: c = √(a² + b²) = √(a² + (area _ 2 / a)²) = √((area _ 2 / b)² + b²)
यह सूत्र उस सूत्र पर आधारित है जिसका उपयोग हम त्रिभुज (a \* b / 2) के क्षेत्रफल की गणना के लिए करते हैं। अन्य दो की तुलना में यह अधिक जटिल लगता है, हालांकि, यह कर्ण की गणना के अन्य दो तरीकों के समान तर्क का पालन करता है।
त्रिकोणमितीय कार्यों के बारे में जानकर अच्छा लगा
यदि आप अभी भी समकोण त्रिभुज के बारे में अधिक जानने के इच्छुक हैं, तो इन त्रिकोणमितीय कार्यों को देखें।
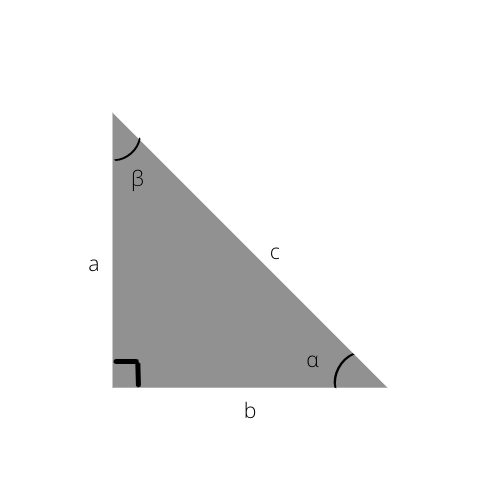
इन्हें जानकर, आप आसानी से समकोण त्रिभुज की भुजाओं की गणना कर सकते हैं, या नीचे दी गई त्रिकोणमितीय तालिका का उपयोग करके कोणों का निर्धारण भी कर सकते हैं।
इसका एक उदाहरण यह हो सकता है कि आप पहले से ही कर्ण और आसन्न का मान जानते हैं; आप आसानी से कोण की कोज्या का पता लगा सकते हैं, फिर सटीक कोण खोजने के लिए ऊपर दी गई तालिका की जांच करें या केवल अनुमान लगाएं कि यह क्या हो सकता है। यदि अल्फा (α) की कोज्या 0.5 है, तो हम जानते हैं कि कोण 60° है।
आप इस विकिपीडिया लेख को भी देख सकते हैं:
भुजाओं के आधार पर त्रिभुजों का वर्गीकरण
1) समबाहु
इस त्रिभुज की तीन बराबर भुजाएँ हैं। इसके परिणामस्वरूप सभी कोण 60° हो जाते हैं।
दृश्य उदाहरण:

समान भुजाओं वाला त्रिकोण
2) समद्विबाहु
इस त्रिभुज में केवल दो भुजाएँ बराबर होती हैं।
दृश्य उदाहरण:

समद्विबाहु त्रिकोण
3) स्केलीन
इस त्रिभुज में कोई भी भुजा समान नहीं है।
दृश्य उदाहरण

विषमबाहु त्रिकोण
कोणों के आधार पर त्रिभुजों का वर्गीकरण
1) एक्यूट
इस त्रिभुज के तीनों कोण 90° से छोटे हैं।
दृश्य उदाहरण:

न्यून त्रिकोण
2) सही
इस त्रिभुज में केवल एक 90° का कोण होता है, जिसके परिणामस्वरूप अन्य दो 90° से कम होते हैं।
क्यों?
α + β + γ = 180° & α = 90° → β + γ = 90° → β , γ < 90°
दृश्य उदाहरण:

सही त्रिकोण
3) अधिक
इस त्रिभुज का एक कोण 90° से बड़ा होता है।
दृश्य उदाहरण:

अधिक त्रिभुज
त्रिकोण के बारे में मजेदार तथ्य
तथ्य 1:
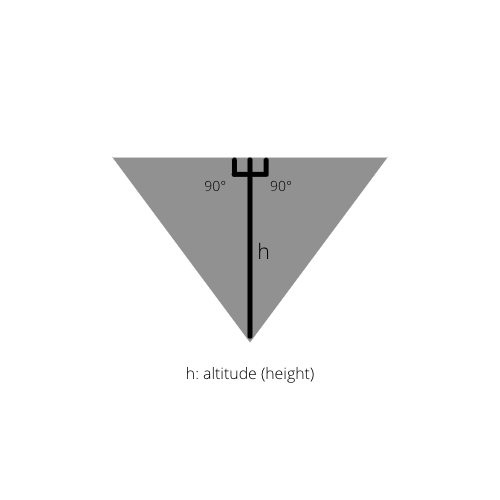
यदि त्रिभुज की आंतरिक-ऊंचाई खींची जाती है, तो हमें मूल त्रिभुज में दो समकोण त्रिभुज प्राप्त होते हैं।
तथ्य 2:
जैसा कि हम जानते हैं, किसी भी त्रिभुज (A) का क्षेत्रफल आधार (A = 1/2 _ b _ h) से गुणा की गई ऊंचाई का आधा होता है। इस सूत्र को समद्विबाहु समकोण त्रिभुज के लिए एक विशेष तरीके से लिखा जा सकता है क्योंकि इसका क्षेत्रफल एक वर्ग के क्षेत्रफल का आधा है।
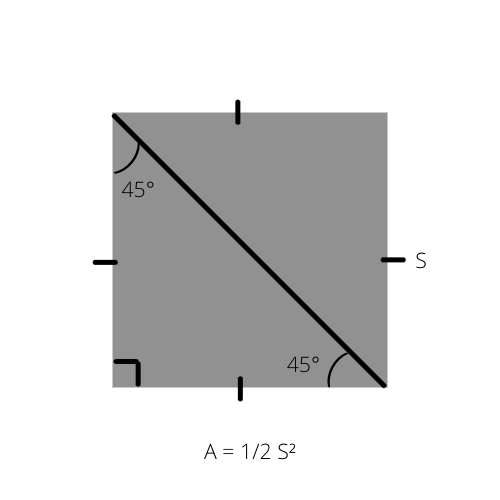
A त्रिभुज का क्षेत्रफल है, और S वर्ग की भुजा है।
तथ्य 3:
त्रिभुज के तीनों कोणों का योग सदैव 180° होता है। यह सभी त्रिभुजों के बारे में सत्य है।
लेख लेखक
Parmis Kazemi
परमिस एक कंटेंट क्रिएटर हैं जिन्हें लिखने और नई चीजें बनाने का शौक है। वह तकनीक में भी अत्यधिक रूचि रखती है और नई चीजें सीखने का आनंद लेती है।
त्रिभुज कर्ण कैलकुलेटर हिन्दी
प्रकाशित: Wed Oct 27 2021
श्रेणी में गणितीय कैलकुलेटर
त्रिभुज कर्ण कैलकुलेटर को अपनी वेबसाइट में जोड़ें
त्रिभुज कर्ण कैलकुलेटर अन्य भाषाओं में
Üçgen Hipotenüs HesaplayıcıKalkulator Hipotenusa SegitigaCalculator De Ipotenuză TriunghiКалькулятар Гіпатэнузы ТрохкутнікаKalkulačka Prepony TrojuholníkaКалкулатор За Хипотенуза На ТриъгълникKalkulator Hipotenuze TrokutaTrikampio Hipotenuzės SkaičiuotuvasCalcolatrice Triangolo IpotenusaTriangle Hypotenuse Calculator