Matemaattiset Laskimet
Kolmion Hypotenuusan Laskin
Selvitä hypotenuusa kaikenlaisille kolmioille helposti ilmaisella matemaattisella laskimellamme!
Kolmion hypotenuusa kahdella sivulla
Kolmion hypotenuusa toiselta sivulta ja alueelta
Sisällysluettelo
Mikä on kolmion hypotenuusa?
Hypotenuusa on kolmion pisin sivu. Se on myös oikeaa kulmaa (90°) vastapäätä.
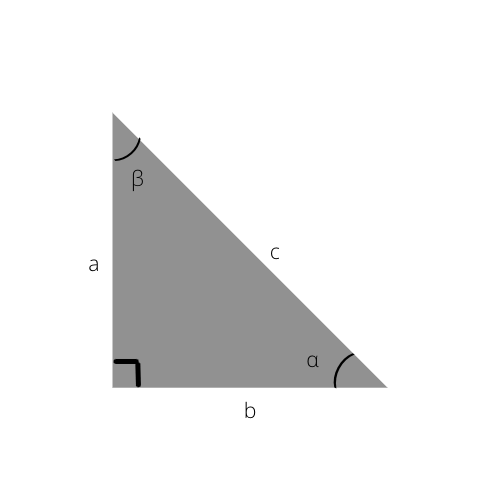
Hypotenuusa on c tässä kolmiossa.
Voit myös lukea tämän Wikipedia-artikkelin:
Miksi hypotenuusa on kolmion pisin sivu?
Tarkasteltuasi yllä olevaa kuvaa ja muita suorakulmioita, huomaat, että hypotenuusa on aina kaikkien suorakulmaisten kolmioiden pisin sivu. Tämä johtuu yksinkertaisesti siitä, että se sijaitsee vastapäätä suurinta kulmaa, 90° kulmaa.
Tämä voidaan myös todistaa matemaattisesti käyttämällä Pythagoraan lausetta:
a² + b² = c²
a² > b² , a² > c²
a > b , a > c
Kuten näet, yllä olevan operaation tulos on, että "a" (hypotenuusa) on suurempi kuin kaksi muuta puolta.
Kuinka laskea kolmion hypotenuusa?
Tämä voidaan tehdä kolmella eri tavalla riippuen annetuista tiedoista, jotka voivat olla muunnelmia alla luetelluista tekijöistä:
a: vastakkainen puoli
b: viereinen puoli
c: hypotenuusan puoli
α: viereisen ja hypotenuusan välinen kulma
β: vastakohdan ja hypotenuusan välinen kulma
1) Kaksi suorakulmaista kolmiojalkaa
Formula: c = √(a² + b²) or c² = a² + b²
Tämä kaava perustuu Pythagoraan lauseeseen, jota voidaan yksinkertaisesti käyttää ottamalla neliöjuuri viereisen ja vastakkaisen neliön summasta.
2) Kulma ja yksi jalka
Formula: c = a / sin(α) = b / sin(β)
Voit myös laskea hypotenuusan käyttämällä sinilakia, joka on tämän kaavan perusta.
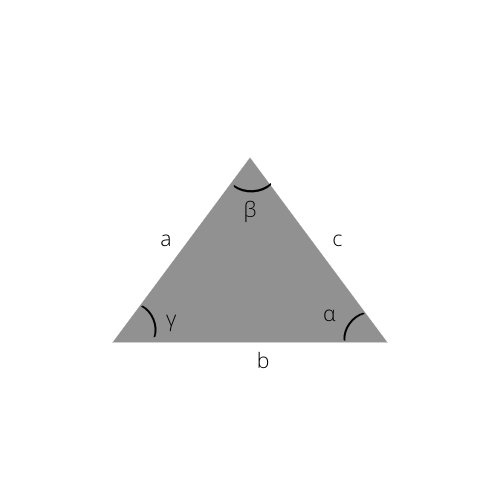
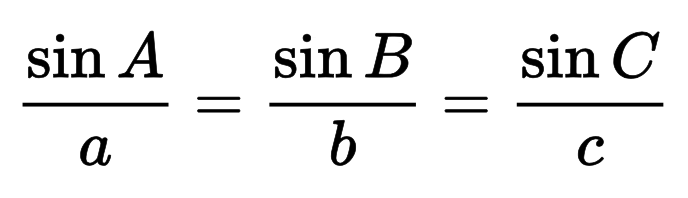
Yleinen sinilaki
3) Alue ja yksi jalka
Formula: c = √(a² + b²) = √(a² + (area _ 2 / a)²) = √((area _ 2 / b)² + b²)
Tämä kaava perustuu kaavaan, jota käytämme kolmion pinta-alan laskemiseen (a \* b / 2). Verrattuna kahteen muuhun se näyttää monimutkaisemmalta, mutta noudattaa samaa logiikkaa kuin kaksi muuta hypotenuusiden laskentatapaa.
Hyvä tietää trigonometrisista funktioista
Jos haluat edelleen tietää enemmän oikeasta kolmiosta, tutustu näihin trigonometrisiin funktioihin.
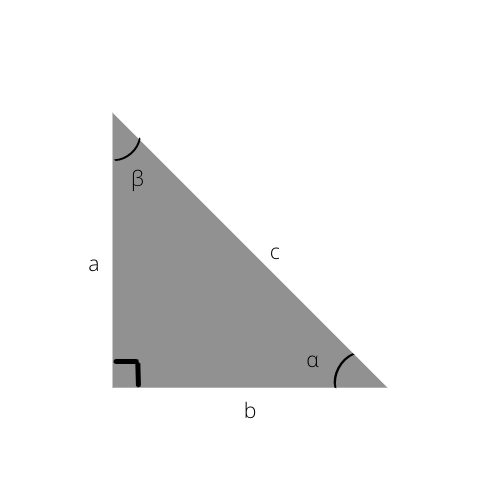
Kun tiedät nämä, voit helposti laskea suoran kolmion sivut tai jopa määrittää kulmat alla olevan trigonometrisen taulukon avulla.
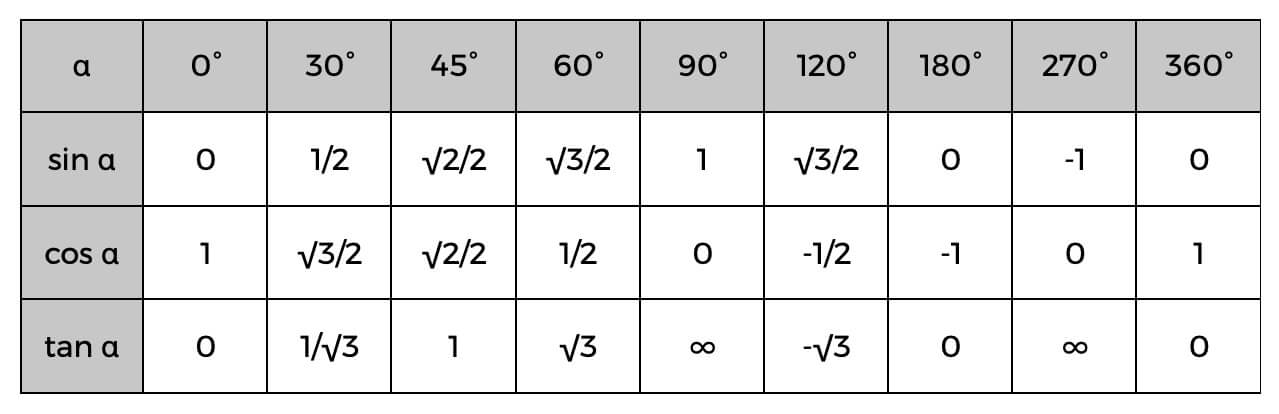
Esimerkki tästä voi olla se, että tiedät jo hypotenuusan ja viereisen arvon; voit helposti löytää kulman kosinin ja tarkista sitten yllä olevasta taulukosta tarkka kulma tai vain arvio siitä, mikä se voisi olla. Jos alfan (α) kosini on 0,5, tiedämme kulman olevan 60°.
Voit myös lukea tämän Wikipedia-artikkelin:
Kolmioiden luokittelu sivujen perusteella
1) Tasasivuinen
Tällä kolmiolla on kolme yhtä suurta sivua. Tämä johtaa siihen, että kaikki kulmat ovat 60°.
Visuaalinen esimerkki:

Tasasivuinen kolmio
2) Tasakylkinen
Tässä kolmiossa vain kaksi sivua ovat yhtä suuret.
Visuaalinen esimerkki:

Tasakylkinen kolmio
3) Scalene
Yksikään sivuista ei ole tasa-arvoinen tässä kolmiossa.
Visuaalinen esimerkki

Skaalaan kolmio
Kolmioiden luokittelu kulmien perusteella
1) Akuutti
Tämän kolmion kaikki kolme kulmaa ovat pienempiä kuin 90°.
Visuaalinen esimerkki:

Terävä kolmio
2) Oikein
Tällä kolmiolla on vain yksi 90° kulma, jolloin kaksi muuta ovat alle 90°.
Miksi?
α + β + γ = 180° & α = 90° → β + γ = 90° → β , γ < 90°
Visuaalinen esimerkki:

Suorakulmainen kolmio
3) Tylsä
Tällä kolmiolla on yksi kulma, joka on suurempi kuin 90°.
Visuaalinen esimerkki:

Tylsä kolmio
Hauskoja faktoja kolmioista
Fakta 1:
Jos kolmion sisäkorkeus piirretään, saadaan alkuperäiseen kolmioon kaksi suorakulmaista kolmiota.
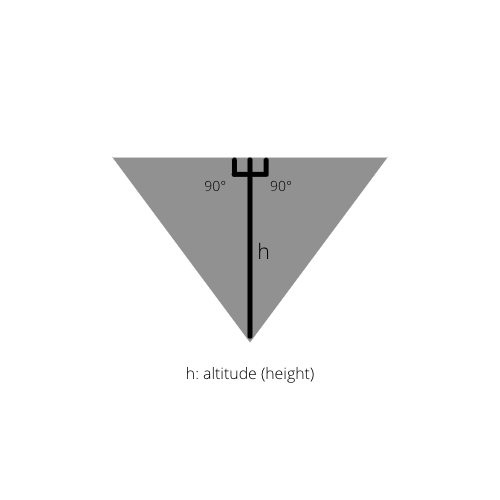
Fakta 2:
Kuten tiedämme, minkä tahansa kolmion (A) pinta-ala on puolet korkeudesta kerrottuna kantalla (A = 1/2 _ b _ h). Tämä kaava voidaan kirjoittaa erityisellä tavalla tasakylkiselle suorakulmaiselle kolmiolle, koska sen pinta-ala on puolet neliön pinta-alasta.
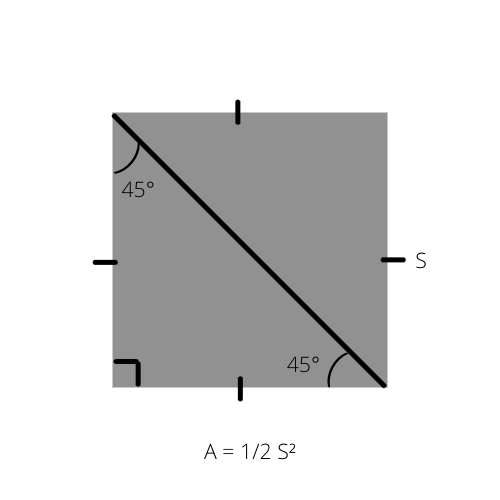
A on kolmion pinta-ala ja S neliön sivu.
Fakta 3:
Kolmion kaikkien kolmen kulman summa on aina 180°. Tämä pätee kaikkiin kolmioihin.
Artikkelin kirjoittaja
Parmis Kazemi
Parmis on sisällöntuottaja, jolla on intohimo kirjoittaa ja luoda uusia asioita. Hän on myös erittäin kiinnostunut tekniikasta ja nauttii uusien asioiden oppimisesta.
Kolmion Hypotenuusan Laskin Suomi
Julkaistu: Wed Oct 27 2021
Luokassa Matemaattiset laskimet
Lisää Kolmion Hypotenuusan Laskin omalle verkkosivustollesi