Matemātiskie Kalkulatori
Trīsstūra Hipotenūzas Kalkulators
Ērti noskaidrojiet hipotenūzu visu veidu trijstūriem, izmantojot mūsu bezmaksas matemātikas kalkulatoru!
Trīsstūra hipotenūza no divām pusēm
Trijstūra hipotenūza vienā pusē un laukums
Satura rādītājs
Kas ir trīsstūra hipotenūza?
Hipotenūza ir trijstūra garākā mala. Tā ir arī pretējā puse no taisnā leņķa (90°).
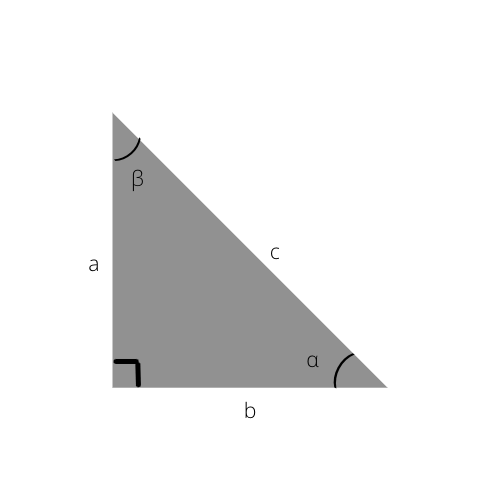
Šajā trīsstūrī hipotenūza ir c.
Varat arī apskatīt šo Wikipedia rakstu:
Kāpēc hipotenūza ir trijstūra garākā mala?
Novērojot iepriekš redzamo attēlu un citus taisnleņķa trijstūrus, jūs ievērosiet, ka hipotenūza vienmēr ir visu taisnleņķa trīsstūru garākā mala. Tas ir vienkārši tāpēc, ka tas atrodas pretī lielākajam leņķim, 90° leņķim.
To var pierādīt arī matemātiski, izmantojot Pitagora teorēmu:
a² + b² = c²
a² > b² , a² > c²
a > b , a > c
Kā redzat, iepriekš minētās darbības rezultāts ir tāds, ka "a" (hipotenūza) ir lielāka par pārējām divām pusēm.
Kā aprēķināt trijstūra hipotenūzu?
To var izdarīt 3 dažādos veidos atkarībā no sniegtās informācijas, kas var būt tālāk uzskaitīto faktoru variācijas.
a: pretējā puse
b: blakus esošā puse
c: hipotenūzas puse
α: leņķis starp blakus esošo un hipotenūzu
β: leņķis starp pretējo un hipotenūzu
1) Divas taisnleņķa trīsstūra kājas
Formula: c = √(a² + b²) or c² = a² + b²
Šīs formulas pamatā ir Pitagora teorēma, kuru var vienkārši izmantot, ņemot kvadrātsakni no blakus un pretējo kvadrātu summas.
2) Leņķis un viena kāja
Formula: c = a / sin(α) = b / sin(β)
Jūs varat arī aprēķināt hipotenūzu, izmantojot sinusa likumu, kas ir šīs formulas pamatā.
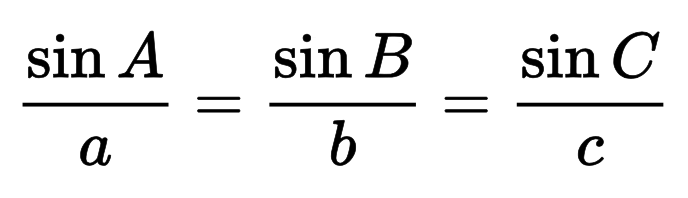
Vispārējais sinusa likums
3) Platība un viena kāja
Formula: c = √(a² + b²) = √(a² + (area _ 2 / a)²) = √((area _ 2 / b)² + b²)
Šīs formulas pamatā ir formula, ko izmantojam, lai aprēķinātu trīsstūra laukumu (a \* b / 2). Salīdzinot ar pārējiem diviem, tas izskatās sarežģītāks, tomēr tas atbilst tādai pašai loģikai kā pārējie divi hipotenūzu aprēķināšanas veidi.
Noderīga informācija par trigonometriskajām funkcijām
Ja jūs joprojām vēlaties uzzināt vairāk par taisnstūra trīsstūri, pārbaudiet šīs trigonometriskās funkcijas.
Zinot tos, varat viegli aprēķināt taisnleņķa trijstūra malas vai pat noteikt leņķus, izmantojot zemāk esošo trigonometrisko tabulu.
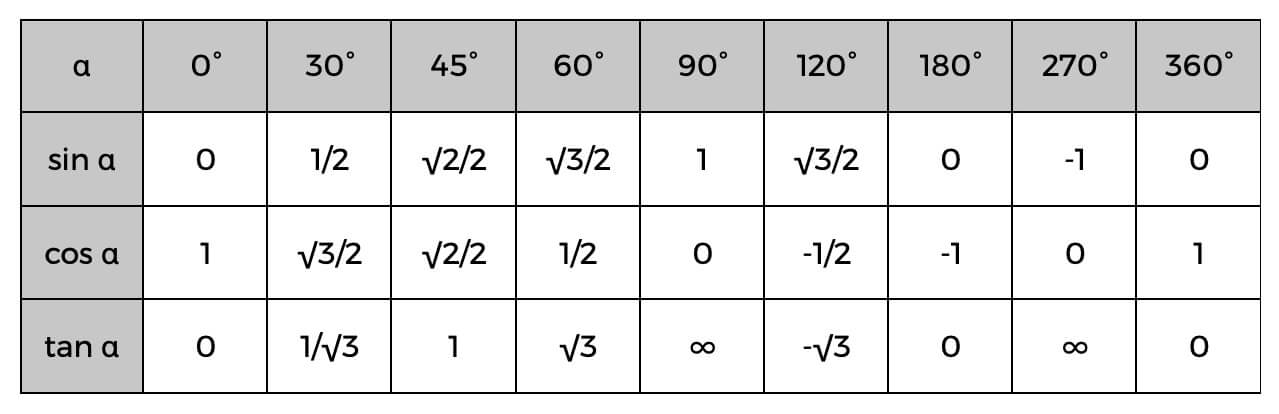
Piemērs tam var būt tas, ka jūs jau zināt hipotenūzas un blakus esošās vērtību; Jūs varat viegli atrast leņķa kosinusu, pēc tam pārbaudiet augstāk esošo tabulu, lai atrastu precīzu leņķi vai tikai aptuvenu, kāds tas varētu būt. Ja alfa (α) kosinuss ir 0,5, tad mēs zinām, ka leņķis ir 60°.
Varat arī apskatīt šo Wikipedia rakstu:
Trīsstūru klasifikācija pēc malām
1) Vienādmalu
Šim trīsstūrim ir trīs vienādas malas. Tā rezultātā visi leņķi ir 60°.
Vizuāls piemērs:

Vienādmalu trīsstūris
2) Vienādsānu
Šajā trīsstūrī tikai divas malas ir vienādas.
Vizuāls piemērs:

Vienādsānu trīsstūris
3) Skalēns
Šajā trīsstūrī neviena no malām nav vienāda.
Vizuāls piemērs

Skalas trīsstūris
Trīsstūru klasifikācija pēc leņķiem
1) Akūts
Visi trīs leņķi šajā trīsstūrī ir mazāki par 90°.
Vizuāls piemērs:

Akūts trīsstūris
2) Pareizi
Šim trīsstūrim ir tikai viens 90° leņķis, kā rezultātā pārējie divi ir mazāki par 90°.
Kāpēc?
α + β + γ = 180° & α = 90° → β + γ = 90° → β , γ < 90°
Vizuāls piemērs:

Taisns trīsstūris
3) Stulbs
Šim trīsstūrim ir viens leņķis, kas ir lielāks par 90°.
Vizuāls piemērs:

Strups trīsstūris
Jautri fakti par trijstūriem
1. fakts:
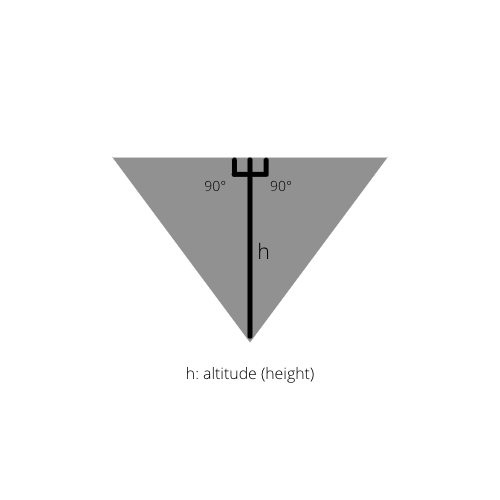
Ja trijstūra iekšējais augstums ir uzzīmēts, mēs iegūstam divus taisnleņķa trīsstūrus sākotnējā trīsstūrī.
2. fakts:
Kā zināms, jebkura trijstūra laukums (A) ir puse no augstuma, kas reizināts ar pamatni (A = 1/2 _ b _ h). Šo formulu var uzrakstīt īpašā veidā vienādsānu taisnstūrim, jo tā laukums ir puse no kvadrāta laukuma.
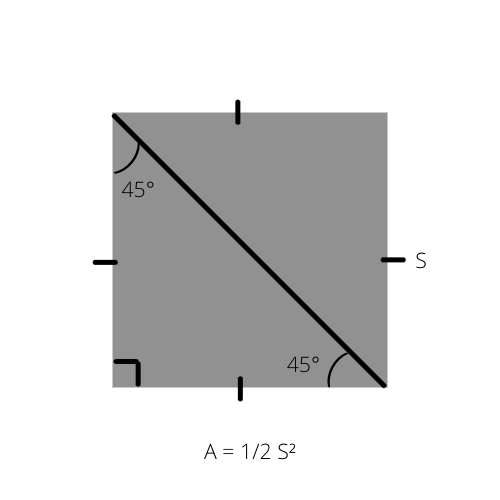
A ir trijstūra laukums un S kvadrāta mala.
3. fakts:
Trijstūra visu trīs leņķu summa vienmēr ir 180°. Tas attiecas uz visiem trīsstūriem.
Raksta autors
Parmis Kazemi
Parmis ir satura veidotājs, kurš aizraujas ar rakstīšanu un jaunu lietu radīšanu. Viņu arī ļoti interesē tehnoloģijas un viņai patīk apgūt jaunas lietas.
Trīsstūra Hipotenūzas Kalkulators Latviešu
Publicēts: Wed Oct 27 2021
Kategorijā Matemātiskie kalkulatori
Pievienojiet Trīsstūra Hipotenūzas Kalkulators savai vietnei