Matemaatilised Kalkulaatorid
Kolmnurga Hüpotenuusi Kalkulaator
Meie tasuta matemaatikakalkulaatoriga saate hõlpsalt teada igasuguste kolmnurkade hüpotenuusid!
Kolmnurga hüpotenuus kahe küljega
Kolmnurga hüpotenuus ühe külje ja pindalaga
Sisukord
Mis on kolmnurga hüpotenuus?
Hüpotenuus on kolmnurga pikim külg. See on ka õige nurga (90°) vastaskülg.
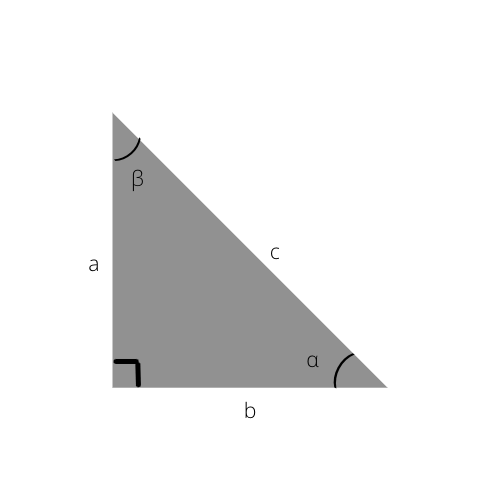
Selle kolmnurga hüpotenuus on c.
Võite vaadata ka seda Wikipedia artiklit:
Miks on hüpotenuus kolmnurga pikim külg?
Pärast ülaltoodud pildi ja teiste täisnurksete kolmnurkade vaatlemist märkate, et hüpotenuus on alati kõigi täisnurksete kolmnurkade pikim külg. Seda lihtsalt seetõttu, et see asub suurima nurga, 90° nurga vastas.
Seda saab tõestada ka matemaatiliselt, kasutades Pythagorase teoreemi:
a² + b² = c²
a² > b² , a² > c²
a > b , a > c
Nagu näete, on ülaltoodud operatsiooni tulemuseks see, et "a" (hüpotenuus) on suurem kui ülejäänud kaks külge.
Kuidas arvutada kolmnurga hüpotenuus?
Seda saab teha kolmel erineval viisil, olenevalt antud teabest, mis võib olla alltoodud tegurite variatsioon.
a: vastaskülg
b: külgnev külg
c: hüpotenuusi pool
α: külgneva ja hüpotenuusi vaheline nurk
β: nurk vastassuuna ja hüpotenuusi vahel
1) Kaks täisnurkset kolmnurga jalga
Formula: c = √(a² + b²) or c² = a² + b²
See valem põhineb Pythagorase teoreemil, mida saab lihtsalt kasutada, võttes ruutjuure külgneva ja vastandi ruutude summast.
2) Nurk ja üks jalg
Formula: c = a / sin(α) = b / sin(β)
Hüpotenuusi saate arvutada ka siinuse seaduse abil, mis on selle valemi aluseks.
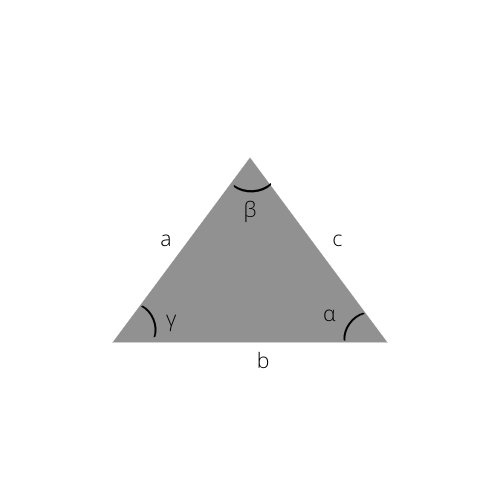
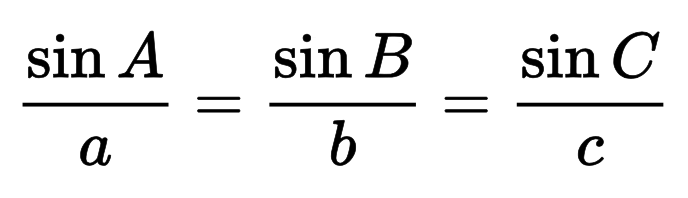
Siinuse üldine seadus
3) Pindala ja üks jalg
Formula: c = √(a² + b²) = √(a² + (area _ 2 / a)²) = √((area _ 2 / b)² + b²)
See valem põhineb valemil, mida kasutame kolmnurga pindala arvutamiseks (a \* b / 2). Võrreldes kahe teisega tundub see keerulisem, kuid järgib sama loogikat nagu kaks ülejäänud hüpotenuuside arvutamise viisi.
Hea teada trigonomeetriliste funktsioonide kohta
Kui soovite ikkagi täisnurkse kolmnurga kohta rohkem teada saada, vaadake neid trigonomeetrilisi funktsioone.
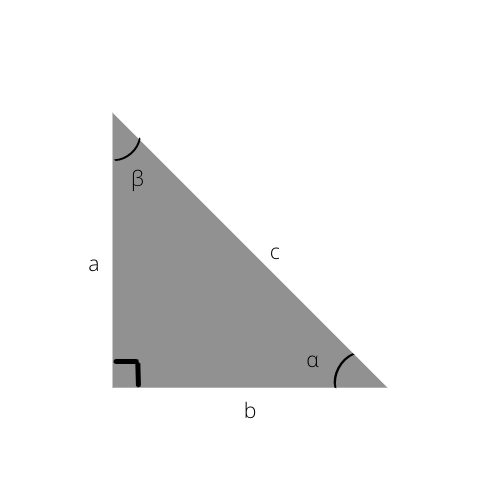
Neid teades saate hõlpsasti arvutada täisnurkse kolmnurga küljed või isegi määrata nurgad alloleva trigonomeetrilise tabeli abil.
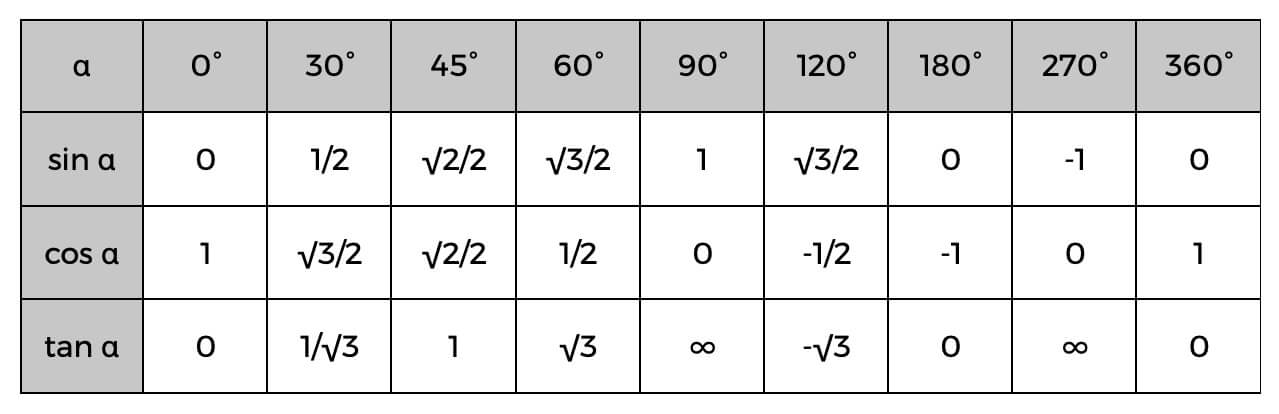
Selle näiteks võib olla see, et te juba teate hüpotenuusi ja külgneva väärtust; saate hõlpsalt leida nurga koosinuse, seejärel kontrollige ülaltoodud tabelit, et leida täpne nurk või lihtsalt hinnang selle kohta, mis see võiks olla. Kui alfa (α) koosinus on 0,5, siis teame, et nurk on 60°.
Võite vaadata ka seda Wikipedia artiklit:
Kolmnurkade klassifitseerimine külgede järgi
1) Võrdkülgne
Sellel kolmnurgal on kolm võrdset külge. Selle tulemusena on kõik nurgad 60°.
Visuaalne näide:

Võrdkülgne kolmnurk
2) Võrdhaarsed
Selles kolmnurgas on ainult kaks külge võrdsed.
Visuaalne näide:

Võrdhaarne kolmnurk
3) Skaleen
Selle kolmnurga ükski külg ei ole võrdne.
Visuaalne näide

Skaleeni kolmnurk
Kolmnurkade klassifitseerimine nurkade alusel
1) Äge
Selle kolmnurga kõik kolm nurka on väiksemad kui 90°.
Visuaalne näide:

Terav kolmnurk
2) Õige
Sellel kolmnurgal on ainult üks 90° nurk, mistõttu ülejäänud kaks on alla 90°.
Miks?
α + β + γ = 180° & α = 90° → β + γ = 90° → β , γ < 90°
Visuaalne näide:

Täisnurkne kolmnurk
3) nüri
Sellel kolmnurgal on üks nurk, mis on suurem kui 90°.
Visuaalne näide:

Nürinurkne kolmnurk
Lõbusaid fakte kolmnurkade kohta
Fakt 1:
Kui tõmmata kolmnurga sisekõrgus merepinnast, saame algses kolmnurgas kaks täisnurkset kolmnurka.
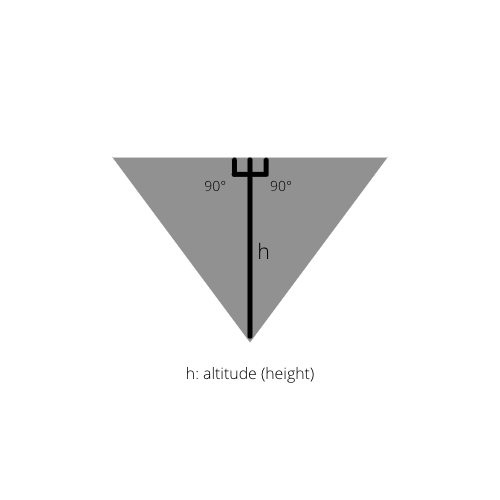
Fakt 2:
Nagu me teame, on iga kolmnurga (A) pindala pool kõrgusest, mis on korrutatud alusega (A = 1/2 _ b _ h). Selle valemi saab kirjutada erilisel viisil võrdhaarse täisnurkse kolmnurga jaoks, kuna selle pindala on pool ruudu pindalast.
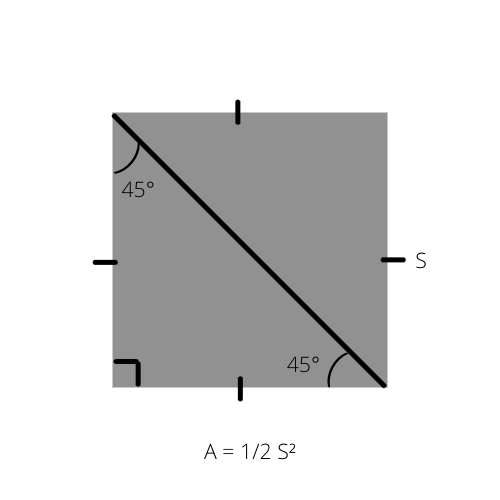
A on kolmnurga pindala ja S on ruudu külg.
Fakt 3:
Kolmnurga kõigi kolme nurga summa on alati 180°. See kehtib kõigi kolmnurkade kohta.
Artikli autor
Parmis Kazemi
Parmis on sisulooja, kellel on kirg kirjutada ja uusi asju luua. Ta on ka väga huvitatud tehnoloogiast ja naudib uute asjade õppimist.
Kolmnurga Hüpotenuusi Kalkulaator Eesti
Avaldatud: Wed Oct 27 2021
Kategoorias Matemaatilised kalkulaatorid
Lisage Kolmnurga Hüpotenuusi Kalkulaator oma veebisaidile