Kalkulatory Matematyczne
Kalkulator Przeciwprostokątnej Trójkąta
Dowiedz się z łatwością przeciwprostokątnej dla wszystkich rodzajów trójkątów dzięki naszemu bezpłatnemu kalkulatorowi matematycznemu!
Trójkąt przeciwprostokątny z dwóch stron
Trójkąt przeciwprostokątny z jednej strony i obszaru
Spis treści
Jaka jest przeciwprostokątna trójkąta?
Przeciwprostokątna to najdłuższy bok trójkąta. Jest to również strona przeciwna do kąta prostego (90°).
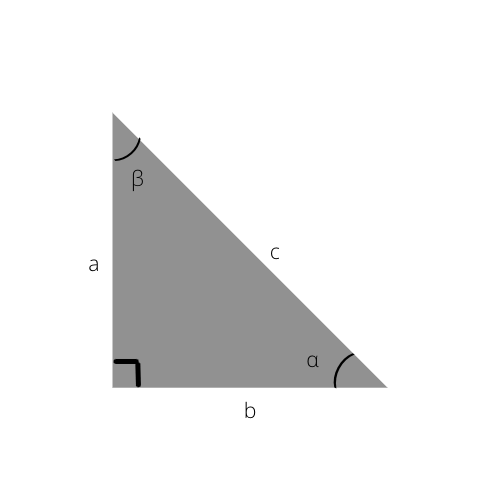
Przeciwprostokątna to c w tym trójkącie.
Możesz również sprawdzić ten artykuł w Wikipedii:
Dlaczego przeciwprostokątna jest najdłuższym bokiem trójkąta?
Obserwując powyższy obrazek i inne trójkąty prostokątne, zauważysz, że przeciwprostokątna jest zawsze najdłuższym bokiem wszystkich trójkątów prostokątnych. Dzieje się tak po prostu dlatego, że znajduje się naprzeciwko największego kąta, kąta 90°.
można to również udowodnić matematycznie za pomocą twierdzenia Pitagorasa:
a² + b² = c²
a² > b² , a² > c²
a > b , a > c
Jak widać, wynik powyższej operacji jest taki, że „a” (przeciwprostokątna) jest większa niż pozostałe dwie strony.
Jak obliczyć przeciwprostokątną trójkąta?
Można to zrobić na 3 różne sposoby, w zależności od podanych informacji, które mogą być odmianą czynników wymienionych poniżej:
A: przeciwna strona
b: sąsiednia strona
c: strona przeciwprostokątna
α: kąt między sąsiednim a przeciwprostokątną
β: kąt między przeciwprostokątną a przeciwprostokątną
1) Dwie prawe trójkątne nogi
Formula: c = √(a² + b²) or c² = a² + b²
Ten wzór jest oparty na twierdzeniu Pitagorasa, które można po prostu wykorzystać, wyciągając pierwiastek kwadratowy z sumy kwadratów sąsiedniego i przeciwnego.
2) Kąt i jedna noga
Formula: c = a / sin(α) = b / sin(β)
Możesz również obliczyć przeciwprostokątną, korzystając z prawa sinusów, które jest podstawą tego wzoru.
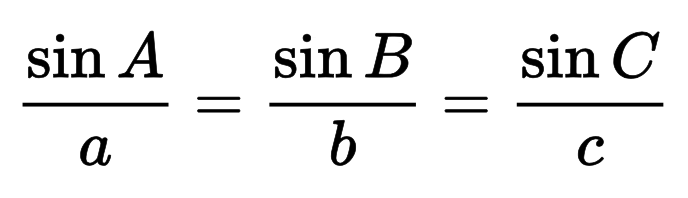
Ogólne prawo sinusów
3) Obszar i jedna noga
Formula: c = √(a² + b²) = √(a² + (area _ 2 / a)²) = √((area _ 2 / b)² + b²)
Ta formuła jest oparta na wzorze, którego używamy do obliczenia pola trójkąta (a \* b / 2). W porównaniu z pozostałymi dwoma wygląda na bardziej skomplikowaną, jednak działa zgodnie z tą samą logiką, co pozostałe dwa sposoby obliczania przeciwprostokątnych.
Dobrze wiedzieć o funkcjach trygonometrycznych
Jeśli nadal chcesz dowiedzieć się więcej o trójkącie prostokątnym, zapoznaj się z tymi funkcjami trygonometrycznymi.
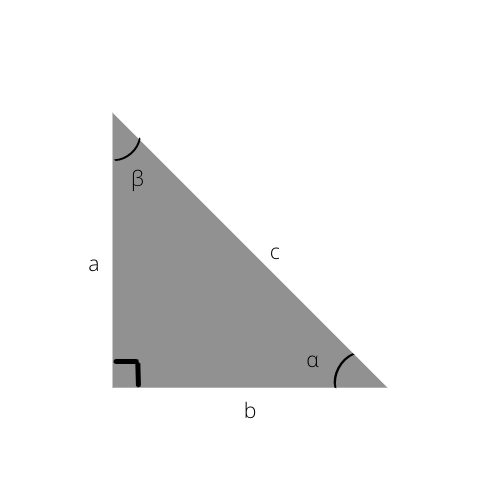
Znając je, możesz łatwo obliczyć boki trójkąta prostokątnego, a nawet określić kąty, korzystając z poniższej tabeli trygonometrycznej.
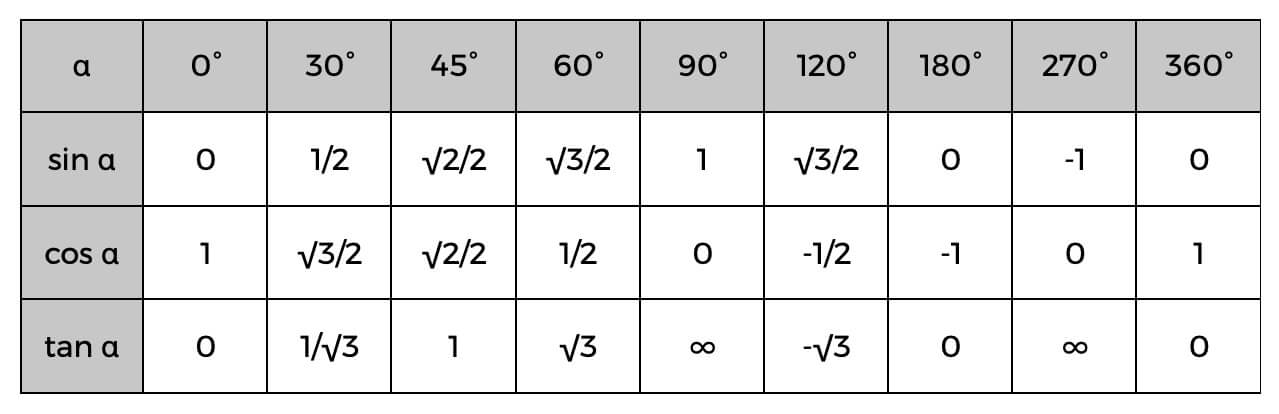
Przykładem może być to, że znasz już wartość przeciwprostokątnej i sąsiedniej; możesz łatwo znaleźć cosinus kąta, a następnie sprawdź powyższą tabelę, aby znaleźć dokładny kąt lub tylko oszacowanie tego, jaki może być. Jeśli cosinus alfa (α) wynosi 0,5, to wiemy, że kąt wynosi 60°.
Możesz również sprawdzić ten artykuł w Wikipedii:
Klasyfikacja trójkątów na podstawie boków
1) Równoboczny
Ten trójkąt ma trzy równe boki. Powoduje to, że wszystkie kąty wynoszą 60°.
Przykład wizualny:

Trójkąt równoboczny
2) równoramienne
W tym trójkącie tylko dwa boki są równe.
Przykład wizualny:

Trójkąt równoramienny
3) Skala
Żaden z boków nie jest równy w tym trójkącie.
Przykład wizualny

Trójkąt skali
Klasyfikacja trójkątów na podstawie kątów
1) Ostre
Wszystkie trzy kąty w tym trójkącie są mniejsze niż 90°.
Przykład wizualny:

Ostry trójkąt
2) Prawo
Ten trójkąt ma tylko jeden kąt 90°, co powoduje, że pozostałe dwa są mniejsze niż 90°.
Czemu?
α + β + γ = 180° & α = 90° → β + γ = 90° → β , γ < 90°
Przykład wizualny:

Trójkąt prostokątny
3) tępy
Ten trójkąt ma jeden kąt większy niż 90°.
Przykład wizualny:

Rozwarty trójkąt
Zabawne fakty na temat trójkątów
Fakt 1:
Jeśli narysujemy wysokość wewnętrzną trójkąta, otrzymamy dwa trójkąty prostokątne w pierwotnym trójkącie.
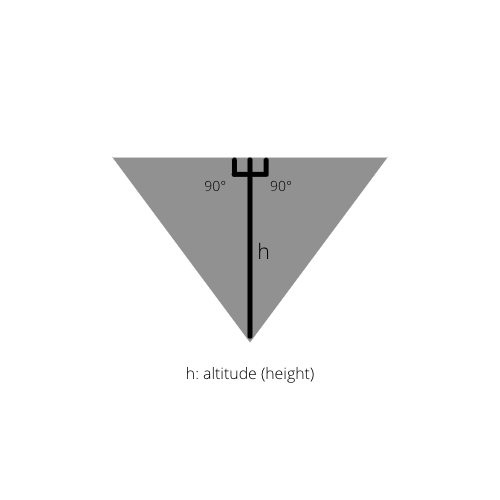
Fakt 2:
Jak wiemy, pole dowolnego trójkąta (A) to połowa wysokości pomnożonej przez podstawę (A = 1/2 _ b _ h). Wzór ten można zapisać w specjalny sposób dla równoramiennego trójkąta prostokątnego, ponieważ jego powierzchnia jest połową pola kwadratu.
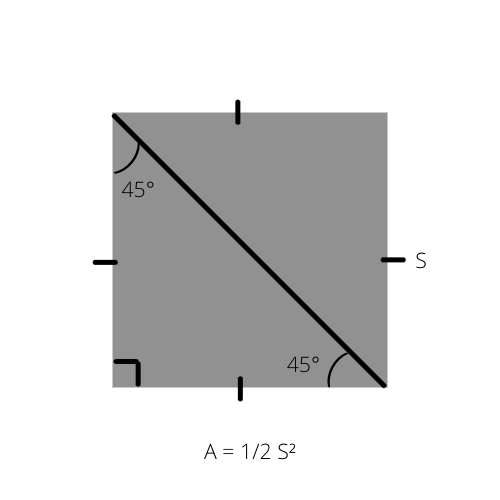
A jest polem trójkąta, a S bokiem kwadratu.
Fakt 3:
Suma wszystkich trzech kątów trójkąta wynosi zawsze 180°. Dotyczy to wszystkich trójkątów.
Autor artykułu
Parmis Kazemi
Parmis to twórca treści, który ma pasję do pisania i tworzenia nowych rzeczy. Jest również bardzo zainteresowana technologią i lubi uczyć się nowych rzeczy.
Kalkulator Przeciwprostokątnej Trójkąta Polski
Opublikowany: Wed Oct 27 2021
W kategorii Kalkulatory matematyczne
Dodaj Kalkulator Przeciwprostokątnej Trójkąta do własnej witryny