Kalkulatory Matematyczne
Kalkulator Prawdopodobieństwa
Kalkulator prawdopodobieństwa umożliwia zbadanie relacji prawdopodobieństwa między dwoma oddzielnymi zdarzeniami. Pozwala to lepiej zrozumieć, w jaki sposób zdarzenia są ze sobą powiązane, a tym samym sprawia, że prognozy są dokładniejsze.
Prawdopodobieństwa pojedynczych zdarzeń
%
%
Jakie prawdopodobieństwo chcesz zobaczyć?
%
Prawdopodobieństwa szeregu zdarzeń
czasy
%
Spis treści
| ◦Definicja prawdopodobieństwa |
| ◦Warunkowe prawdopodobieństwo |
| ◦Prawdopodobieństwo teoretyczne a eksperymentalne |
| ◦Prawdopodobieństwo i statystyka |
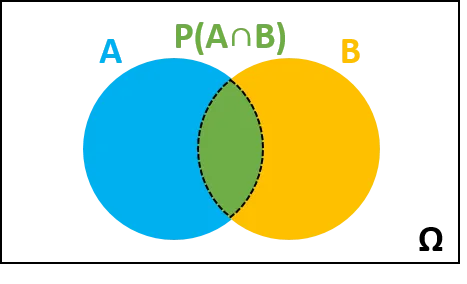
Kalkulator prawdopodobieństwa jest pomocnym narzędziem podczas badania relacji między zdarzeniami, takimi jak prawdopodobieństwo zajścia zdarzenia A i prawdopodobieństwo zajścia zdarzenia B. Na przykład, jeśli szansa na zajście zdarzenia A wynosi 50% i jest taka sama dla zdarzenia B, jakie są szanse na zajście obu zdarzeń, tylko jednego zdarzenia, co najmniej jednego zdarzenia lub żadnego z nich i tak dalej?
Nasz kalkulator prawdopodobieństwa pomaga zobaczyć prawdopodobieństwo sześciu różnych scenariuszy. Dodatkowo, gdy wpiszesz, ile razy „kostka została rzucona”, otrzymasz cztery dodatkowe scenariusze. W ten sposób nie musisz samodzielnie wykonywać wszystkich obliczeń. Po prostu wpisz liczby, a nasz kalkulator zajmie się resztą!
Definicja prawdopodobieństwa
Prawdopodobieństwo jest sposobem myślenia o niepewnych sytuacjach i jest wykorzystywane w różnych dziedzinach, takich jak hazard, podejmowanie decyzji i statystyki. Definicja prawdopodobieństwa podana w tym kursie jest najbardziej podstawową i fundamentalną definicją przedmiotu.
Warunkowe prawdopodobieństwo
Prawdopodobieństwo polega na badaniu przypadku, a jednym z najważniejszych pojęć do zrozumienia jest to, czy zdarzenia są zależne, czy nie. Dwa zdarzenia są niezależne, jeśli wystąpienie pierwszego nie wpływa na prawdopodobieństwo wystąpienia drugiego. Jest to niezwykle ważne, ponieważ określa, w jaki sposób możemy obliczyć potencjalne wyniki. Jeśli rzucimy doskonale wyważoną standardową sześcienną kostką, istnieje 1/6 szansy na otrzymanie dwójki.
Mimo że w tym przykładzie kości zostały połączone, prawdopodobieństwo uzyskania dwójki ⚁ w drugiej turze nadal wynosi 1/6, ponieważ zdarzenia są niezależne. Oznacza to, że prawdopodobieństwo uzyskania co najmniej jednego konkretnego wyniku, na przykład dwójki ⚁ w pierwszej turze, nie zależy od tego, co dzieje się z kostkami w drugiej turze.
W prawdopodobieństwie istnieją różne sposoby patrzenia na scenariusz. Tym razem porozmawiamy o prawdopodobieństwie warunkowym. Załóżmy, że grasz w tenisa i jeden z twoich przeciwników zbliża się do siatki. W zależności od kąta, pod jakim uderzą piłkę, może być możliwe wysłanie piłki obok przeciwnika jednym strzałem. Jeśli jednak ich przeciwnik uchyli się, gdy zobaczy nadchodzącą piłkę, piłka prawdopodobnie odbije się od ziemi, a przeciwnik może ją złapać. Jest to przykład sytuacji, w której myślenie o grze w kategoriach zdarzeń (uderzenia piłki) i wyników.
Prawdopodobieństwo teoretyczne a eksperymentalne
W większości przypadków prawdopodobieństwo teoretyczne definiuje się jako stosunek liczby korzystnych wyników do liczby wszystkich możliwych wyników. Istnieje jednak różnica między prawdopodobieństwem teoretycznym a prawdopodobieństwem eksperymentalnym. Formalna definicja prawdopodobieństwa eksperymentalnego to stosunek liczby wyników należących do określonej kategorii (eksperymentu) do całkowitej liczby wyników. Projekt eksperymentu opiera się na podanych informacjach, logicznym rozumowaniu i mówieniu nam, czego możemy się spodziewać po eksperymencie. Idealnie byłoby, gdyby informacje te pochodziły z testowanej hipotezy. Po zebraniu tych informacji projekt eksperymentu pomoże ci zaprojektować eksperyment w sposób, który potwierdzi lub obali twoją hipotezę.
W grze 42 kulek jedna kula jest losowo wybierana i wkładana z powrotem do torby nieskończoną liczbę razy. Oznacza to, że w woreczku zawsze są 42 kule, z których 18 jest pomarańczowych. Możemy obliczyć prawdopodobieństwo wylosowania konkretnego koloru, dzieląc liczbę kulek tego koloru przez całkowitą liczbę kulek w woreczku (42). Upraszcza się to do 3/7, czyli prawdopodobieństwo wynosi 18/42, co oznacza, że na każde 14 zebranych piłek powinny być 3 pomarańczowe kule.
Prawdopodobieństwo jest nauką matematyczną, która zajmuje się prawdopodobieństwem wystąpienia czegoś. Może służyć do przewidywania, co stanie się w wyniku przeprowadzenia eksperymentu, lub do zrozumienia prawdopodobieństwa wystąpienia czegoś w danej sytuacji. W tym przykładzie użyjemy eksperymentalnego prawdopodobieństwa, aby zrozumieć, co się stało, gdy wyjęliśmy kulkę z torby i powtórzyliśmy tę procedurę jeszcze 13 razy. Załóżmy, że mamy 8 pomarańczowych kulek w 14 próbach. Daje nam to empiryczne prawdopodobieństwo 8 na 14, czyli 44%.
Będą chwile, kiedy wybierzesz więcej kart, chwile, kiedy dostaniesz mniej, i chwile, kiedy wybierzesz przewidywaną liczbę. Wynik będzie jednak odbiegał od teoretycznego. Dzieje się tak, ponieważ kiedy będziesz powtarzać tę grę w kółko, czasami wybierzesz więcej, a czasami mniej, a czasami wybierzesz dokładnie liczbę przewidzianą teoretycznie. Jeśli zsumujesz wszystkie wyniki, powinieneś zauważyć, że ogólne prawdopodobieństwo zbliża się coraz bardziej do prawdopodobieństwa teoretycznego. Jeśli nie, może wystąpić rozbieżność między tym, co widzisz, a hipotetycznym wynikiem — może tak być na przykład, jeśli niektóre kule w worku mają różne kolory i rozmiary. Aby uzyskać dokładne oszacowanie, musisz przeprowadzić losowy proces selekcji.
Prawdopodobieństwo i statystyka
Statystyka to dział matematyki zajmujący się gromadzeniem, interpretacją, analizą, prezentacją i interpretacją danych. Prawdopodobieństwo jest gałęzią matematyki, która bada możliwość zdarzeń i ich skutki. Ważne jest, aby zrozumieć te różnice, ponieważ mogą one prowadzić do różnych wniosków w różnych sytuacjach.
Prawdopodobieństwo to teoretyczna dziedzina matematyki, która zajmuje się takimi rzeczami, jak definicje i twierdzenia matematyczne. W przeciwieństwie do tego, statystyka jest praktycznym zastosowaniem matematyki, które próbuje przypisać sens i zrozumienie obserwacjom w prawdziwym świecie. Statystykę można podzielić na dwie główne gałęzie – opisową i inferencyjną. Statystyki opisowe badają właściwości opisowe populacji, takie jak liczebność, średnie i odchylenia standardowe. Statystyki inferencyjne wykorzystują metody statystyczne do wyciągania wniosków na temat populacji na podstawie próbek z eksperymentu lub obserwacji pobranych z rzeczywistego świata.
Prawdopodobieństwo to zdolność przewidywania możliwości zdarzeń, podczas gdy statystyka to badanie częstotliwości zdarzeń w przeszłości. Pod koniec kursu będziesz miał głębsze zrozumienie tych koncepcji i będziesz w stanie wykorzystać je do modelowania rzeczywistych danych.
Załóżmy, że grasz w grę losową, w której każda karta jest wybierana z takim samym prawdopodobieństwem, a Twoim celem jest wygrana. W takim przypadku możesz postawić zakład na podstawie kursu - czyli prawdopodobieństwa, że wybraną przez Ciebie kartą będzie pik. Zakładając, że talia jest kompletna, a wybór jest całkowicie losowy i sprawiedliwy, można wywnioskować, że prawdopodobieństwo wynosi ¼. Oznacza to, że możesz śmiało postawić zakład.
Statystyk będzie obserwował grę przez chwilę, aby ocenić uczciwość, zanim skonsultuje się z probabilistą, jakie działania należy podjąć, aby mieć największe szanse na wygraną. Po tym, jak uznają, że gra jest tego warta, probabilista doradzi, jakie kroki podjąć, aby zwiększyć swoje szanse.
Autor artykułu
John Cruz
John jest doktorantem z pasją do matematyki i edukacji. W wolnym czasie John lubi wędrować i jeździć na rowerze.
Kalkulator Prawdopodobieństwa Polski
Opublikowany: Sun Jan 08 2023
W kategorii Kalkulatory matematyczne
Dodaj Kalkulator Prawdopodobieństwa do własnej witryny