Matemātiskie Kalkulatori
Varbūtību Kalkulators
Varbūtības kalkulators ļauj izpētīt varbūtības attiecības starp diviem atsevišķiem notikumiem. Tas ļauj labāk izprast, kā notikumi ir saistīti, un tādējādi prognozes kļūst precīzākas.
Atsevišķu notikumu varbūtības
%
%
Kādu varbūtību vēlaties redzēt?
%
Notikumu sērijas varbūtības
reizes
%
Satura rādītājs
| ◦Varbūtības definīcija |
| ◦Nosacītā varbūtība |
| ◦Teorētiskā vs eksperimentālā varbūtība |
| ◦Varbūtība un statistika |
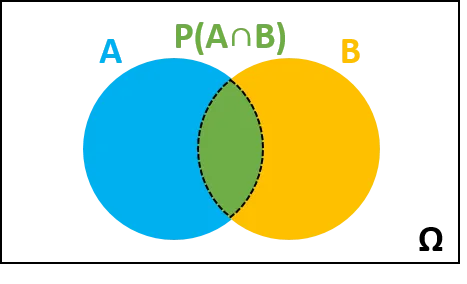
Varbūtības kalkulators ir noderīgs rīks, pētot sakarības starp notikumiem, piemēram, A iespējamību un B iespējamību. Piemēram, ja iespēja, ka A notiks, ir 50%, un tas pats B, kāda ir iespēja, ka notiks abi, notiks tikai viens, vismaz viens, vai nenotiks neviens un tā tālāk?
Mūsu varbūtības kalkulators palīdz jums redzēt sešu dažādu scenāriju iespējamību. Turklāt, ievadot, cik reižu "mets ir nomests", tiek parādīti vēl četri scenāriji. Tādā veidā jums nav jāveic visi aprēķini pašam. Vienkārši ierakstiet skaitļus, un mūsu kalkulators parūpēsies par pārējo!
Varbūtības definīcija
Varbūtība ir domāšanas veids par nenoteiktām situācijām, un to izmanto dažādās jomās, piemēram, azartspēlēs, lēmumu pieņemšanā un statistikā. Šajā kursā sniegtā varbūtības definīcija ir visvienkāršākā un fundamentālākā priekšmeta definīcija.
Nosacītā varbūtība
Varbūtība ir saistīta ar nejaušības izpēti, un viens no vissvarīgākajiem jēdzieniem, kas jāsaprot, ir tas, vai notikumi ir atkarīgi vai nē. Divi notikumi ir neatkarīgi, ja pirmā iestāšanās neietekmē otrā iestāšanās iespējamību. Tas ir neticami svarīgi, jo tas nosaka, kā mēs varam aprēķināt iespējamos rezultātus. Ja metīsim perfekti līdzsvarotu standarta kauliņu, pastāv 1/6 iespēja iegūt divnieku.
Lai gan šajā piemērā kauliņi ir sasaistīti, varbūtība iegūt divi ⚁ otrajā pagriezienā joprojām ir 1/6, jo notikumi ir neatkarīgi. Tas nozīmē, ka varbūtība iegūt vismaz vienu konkrētu rezultātu, piemēram, divi⚁ pirmajā gājienā, nav atkarīga no tā, kas notiek ar kauliņu otrajā gājienā.
Visticamāk, scenāriju var aplūkot dažādi. Šoreiz mēs runāsim par nosacīto varbūtību. Pieņemsim, ka jūs spēlējat tenisa spēli un kāds no jūsu pretiniekiem tuvojas tīklam. Atkarībā no leņķa, kādā viņi sit bumbu, var būt iespējams nosūtīt bumbu garām pretiniekam vienā sitienā. Tomēr, ja viņu pretinieks pielec, redzot bumbu, bumba, visticamāk, atlēks no zemes un pretinieks to varētu noķert. Šis ir piemērs situācijai, kad domā par spēli notikumu (bumbiņas sitiena) un iznākumu izteiksmē.
Teorētiskā vs eksperimentālā varbūtība
Vairumā gadījumu teorētiskā varbūtība tiek definēta kā attiecība starp labvēlīgo iznākumu skaitu un visu iespējamo iznākumu skaitu. Tomēr pastāv atšķirība starp teorētisko varbūtību un eksperimentālo varbūtību. Formālā eksperimentālās varbūtības definīcija ir attiecība starp rezultātu skaitu, kas ietilpst noteiktā kategorijā (eksperimentā), un kopējo rezultātu skaitu. Eksperimentālā plānošana balstās uz sniegto informāciju, loģisku argumentāciju un stāsta, ko sagaidīt no eksperimenta. Ideālā gadījumā šī informācija tiks iegūta no pārbaudāmās hipotēzes. Pēc šīs informācijas apkopošanas eksperimentālais dizains palīdzēs jums izveidot eksperimentu tā, lai apstiprinātu vai atceltu jūsu hipotēzi.
42 bumbiņu spēlē nejauši tiek izvēlēta viena bumbiņa un bezgalīgi daudz reižu ielikta atpakaļ somā. Tas nozīmē, ka somā vienmēr ir 42 bumbiņas, no kurām 18 ir oranžas. Mēs varam aprēķināt konkrētas krāsas izvēles varbūtību, dalot šīs krāsas bumbiņu skaitu ar kopējo bumbiņu skaitu maisā (42). Tas ir vienkāršots līdz 3/7 vai varbūtība ir 18/42, kas nozīmē, ka no katrām 14 atlasītajām bumbiņām jābūt 3 oranžām bumbiņām.
Varbūtība ir matemātikas zinātne, kas pēta iespēju, ka kaut kas notiks. To var izmantot, lai paredzētu, kas notiks eksperimenta veikšanas rezultātā, vai lai saprastu izredzes, ka kaut kas notiks noteiktā situācijā. Šajā piemērā mēs izmantosim eksperimentālo varbūtību, lai saprastu, kas notika, kad no maisiņa izņēmām marmoru un atkārtojām procedūru vēl 13 reizes. Pieņemsim, ka 14 mēģinājumos esam ieguvuši 8 oranžas bumbiņas. Tas dod mums empīrisko varbūtību 8 no 14 jeb 44%.
Būs brīži, kad izvēlēsities vairāk kāršu, reizes, kad saņemsit mazāk, un reizes, kad izvēlēsities paredzēto numuru. Rezultāts tomēr atšķirsies no teorētiskā. Tas notiek tāpēc, ka, mēģinot atkārtot šo spēli atkal un atkal, dažreiz jūs izvēlaties vairāk, dažreiz jūs saņemsiet mazāk, un dažreiz jūs izvēlēsities tieši teorētiski paredzēto skaitli. Ja jūs summējat visus rezultātus, jums vajadzētu pamanīt, ka kopējā varbūtība kļūst arvien tuvāk teorētiskajai varbūtībai. Ja nē, tad var būt neatbilstība starp to, ko jūs redzat, un hipotētisko iznākumu – tā varētu būt, piemēram, ja dažas bumbiņas somā ir dažādu krāsu un izmēru. Lai iegūtu precīzu aprēķinu, atlases process būs jāveic nejauši.
Varbūtība un statistika
Statistika ir matemātikas nozare, kas nodarbojas ar datu vākšanu, interpretāciju, analīzi, prezentāciju un interpretāciju. Varbūtība ir matemātikas nozare, kas pēta notikumu iespējamību un to iznākumus. Ir svarīgi saprast šīs atšķirības, jo dažādās situācijās no tām var izdarīt dažādus secinājumus.
Varbūtība ir teorētisks matemātikas lauks, kas nodarbojas ar tādām lietām kā matemātiskas definīcijas un teorēmas. Turpretim statistika ir praktisks matemātikas pielietojums, kas mēģina piedēvēt novērojumu jēgu un izpratni par reālajā pasaulē. Statistiku var iedalīt divās galvenajās nozarēs – aprakstošajā un secinošajā. Aprakstošā statistika pārbauda populācijas aprakstošās īpašības, piemēram, skaitu, vidējos rādītājus un standarta novirzes. Secinošā statistika izmanto statistikas metodes, lai no paraugiem izdarītu secinājumus par populāciju vai nu no eksperimenta, vai no novērojumiem, kas ņemti no reālās pasaules.
Varbūtība ir spēja paredzēt notikumu iespējamību, savukārt statistika ir pagātnes notikumu biežuma izpēte. Kursa beigās jūs iegūsit dziļāku izpratni par šiem jēdzieniem un varēsiet tos izmantot, lai modelētu reālās pasaules datus.
Pieņemsim, ka jūs spēlējat azartspēli, kurā katra kārts tiek izvēlēta ar vienādu varbūtību, un jūsu mērķis ir uzvarēt. Šajā gadījumā jūs varētu veikt likmi, pamatojoties uz koeficientu - tas ir, varbūtību, ka jūsu izvēlētā kārts būs pīķa. Pieņemot, ka komplekts ir pilnīgs un izvēle ir pilnīgi nejauša un taisnīga, jūs varētu secināt, ka varbūtība ir vienāda ar ¼. Tas nozīmē, ka varat droši veikt likmi.
Statistiķis kādu laiku vēros spēli, lai novērtētu godīgumu, pirms konsultēsies ar varbūtības uzņēmēju par to, kādas darbības jāveic, lai būtu vislielākā iespēja uzvarēt. Pēc tam, kad viņi piekrīt, ka spēle ir tā vērta, varbūtības eksperts ieteiks, kā rīkoties, lai uzlabotu savas izredzes.
Raksta autors
John Cruz
Džons ir doktorants un aizraujas ar matemātiku un izglītību. Brīvajā laikā Džonam patīk doties pārgājienos un braukt ar velosipēdu.
Varbūtību Kalkulators Latviešu
Publicēts: Sun Jan 08 2023
Kategorijā Matemātiskie kalkulatori
Pievienojiet Varbūtību Kalkulators savai vietnei