Matemātiskie Kalkulatori
Trigonometrijas Kalkulators
Aprēķiniet viegli trigonometriskās vērtības Sin, Cos, Tan, Cot, Sec un Csc, izmantojot mūsu bezmaksas tiešsaistes kalkulatoru!
Trigonometrijas kalkulators
Satura rādītājs
Kas ir trigonometrija?
Trigonometrija ir matemātikas nozare, kas nodarbojas ar trijstūra malām un leņķiem. Šis temats aptver arī attiecīgās funkcijas, ko izmanto leņķu aprēķināšanai.
Kādas ir primārās vai pamata trigonometriskās funkcijas?
Zemāk jūs redzēsiet galveno trigonometrisko funkciju sarakstu, kuras galvenokārt tiek izmantotas, izmantojot trigonometriju.
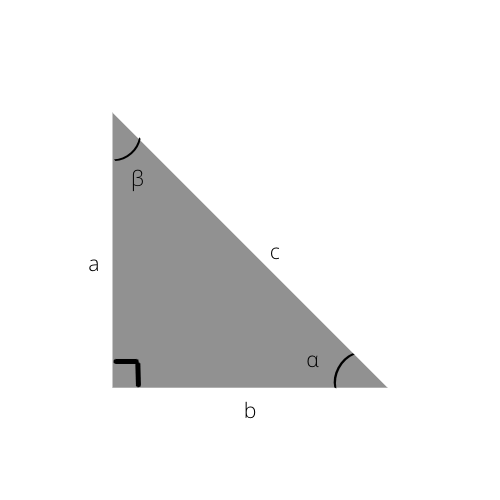
Taisnstūra trīsstūra piemērs. "α" leņķis šajā attēlā ir norādīts tālāk norādītajās formulās.
1) Leņķa sinuss
Formula: sin α = pretējs / hipotenūza
Leņķa sinusa attiecība taisnleņķa trijstūra kontekstā ir pretēja garums dalīts ar hipotenūzas garumu.
2) Leņķa kosinuss
Formula: cos α = blakus / hipotenūza
Leņķa kosinusu taisnleņķa trīsstūra kontekstā aprēķina, dalot blakus esošā garumu ar hipotenūzas garumu.
3) Leņķa pieskare
Formula: tan α = sin α / cos α = pretējs / blakus
Leņķa tangensu taisnleņķa trijstūra kontekstā aprēķina, dalot sinusu ar kosinusu. To var arī aizstāt, dalot pretējo ar blakus esošo.
Lietojot šīs funkcijas, ņemiet vērā arī trigonometrisko tabulu.
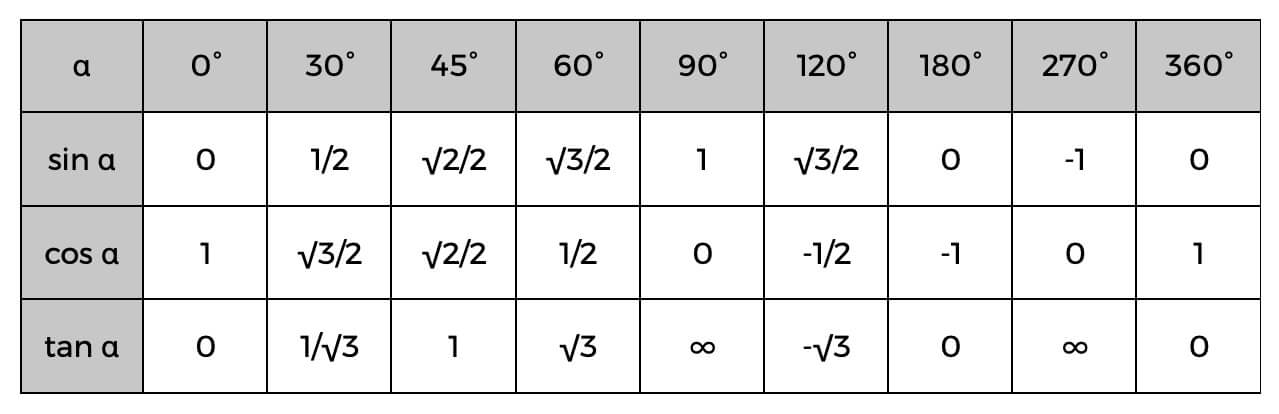
Trigonometriskā tabula
Kas ir abpusējas trigonometriskās funkcijas?
Papildus primārajām trigonometriskajām funkcijām ir arī cita funkciju kopa, kas nav tik izmantota, salīdzinot ar pirmo kategoriju. Tie ietver sekantu (sec), kosekantu (csc) un kotangensu (cot).
Kam tiek izmantota trigonometrija?
Trigonometrija ir saistīta ar trijstūriem, jo īpaši taisnstūriem. Tāpēc visur, kur redzat trīsstūri ārpus matemātikas pasaules, varat derēt, ka trigonometrija ir noderīga. Piemērs tam ir trigonometrisko aprēķinu izmantošana tādās jomās kā arhitektūra, astronomija un ķīmijas inženierija.
Reālās dzīves trigonometrijas pielietojumi
Izņemot acīmredzamo trigonometrijas izmantošanu, kas ir matemātikā, trigonometriju izmanto arī reālās dzīves situācijās un laukos.
1) Arhitektūra un inženierija
Nav pārāk tālu domāt par trigonometrisko funkciju izmantošanu arhitektūrā. Šīs funkcijas galvenokārt tiek izmantotas, lai aprēķinātu diagonālā savienojuma garumu, kas savieno divas līnijas. To izmanto, lai aprēķinātu jumta slīpuma diagonālo garumu, projektējot slīpu jumtu. Jums tikai jāzina jumta augstums un garums, un jūs varat doties uz!

2) Astronomija
Astronomija ir svarīgs priekšmets, kam vecās kultūras lielākoties pievērsa uzmanību. Runājot par to, iespējams, viena no pirmajām lietām, kas nāk prātā, ir zvaigznāji un to attāluma aprēķināšana viens no otra un citiem objektiem kosmosā, kas ir viens no vienkāršākajiem astronomijas lietojumiem. Citiem vārdiem sakot, trigonometriju var izmantot, lai aprēķinātu saules un zemes attālumu no dažādām zvaigznēm. Zvaigžņu attālums ir svarīgs, lai aprēķinātu to faktorus astronomijas pasaulē.
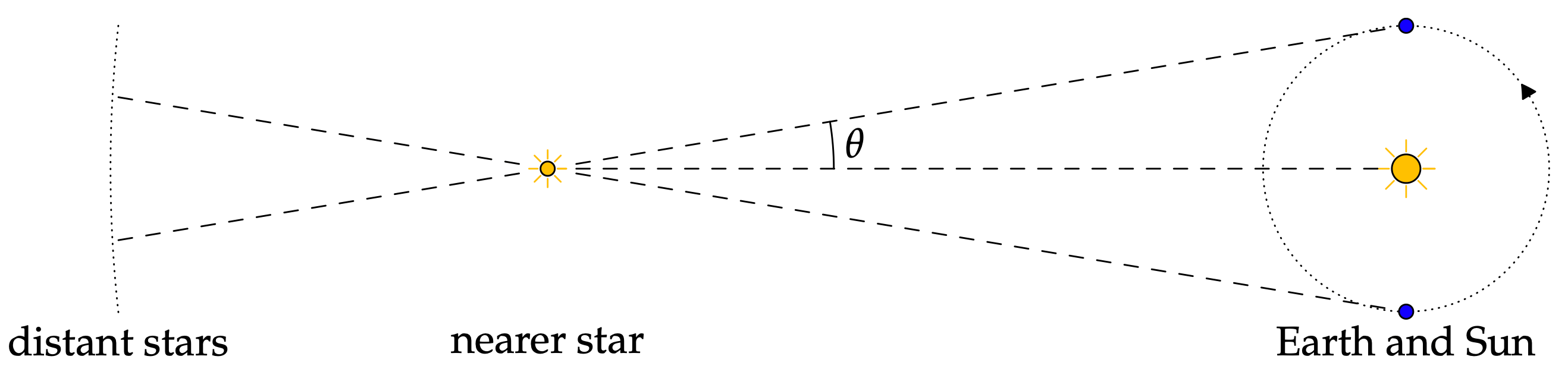
Papildinformāciju par astronomiju un tās saistību ar trigonometriju skatiet šajā rakstā:
3) Elektronika un elektrotehnika
Trigonometriju izmanto matemātikas problēmu risināšanai elektronikā un elektrotehnikā, galvenokārt, veidojot modeli. Vēl viens svarīguma piemērs ir, veicot estētiskus papildinājumus un pārliecinoties, ka tie netraucē modeļa darbību.
Tomēr trigonometriskās funkcijas ļoti noder, strādājot ar shēmām. Skatiet tālāk redzamo vizuālo piemēru, lai iegūtu turpmāku demonstrāciju un iegūtu priekšstatu par to, kā trigonometrija pārvēršas ķēdes loģikā.
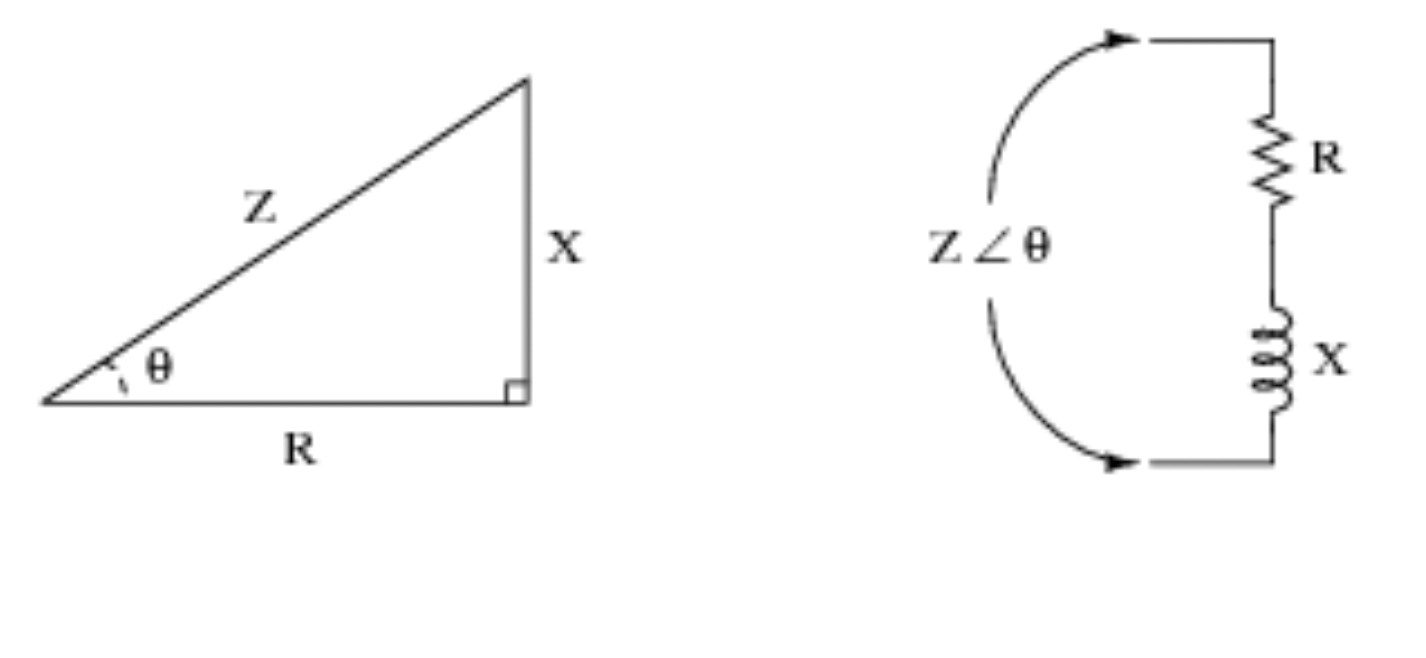
4) Seismoloģija
Seismoloģija pēta zemestrīces, kā arī seismiskos viļņus, kas pārvietojas pa zemi un ap to. Trigonometrija tiek izmantota, lai atvieglotu seismiskā viļņa vertikālā un horizontālā attāluma aprēķināšanu.

5) Mērniecība (civilā inženierija)
Mērniecība ir bijusi profesija, kas pastāv jau ilgu laiku, vismaz tik ilgi, cik rāda ierakstītā vēsture. To veic mērnieks, kura uzdevums ir precīzi izmērīt zemes virsmas lielā mērogā. Iespējams, jau uzminējāt trigonometrijas izmantošanu; būtībā trigonometrija tiek izmantota, kad mērniekam ir jāaprēķina ainavas objektu garums, platības un relatīvie leņķi.
Tālāk sniegtais piemērs ir labs iepriekš izskaidrotā vizuālais demonstrējums. Mērnieks izmanto trigonometriskās daļas, lai aprēķinātu savu attālumu no kalna virsotnes vai no jebkuras citas vietas, ko izvēlas.

Raksta autors
Parmis Kazemi
Parmis ir satura veidotājs, kurš aizraujas ar rakstīšanu un jaunu lietu radīšanu. Viņu arī ļoti interesē tehnoloģijas un viņai patīk apgūt jaunas lietas.
Trigonometrijas Kalkulators Latviešu
Publicēts: Fri Oct 29 2021
Kategorijā Matemātiskie kalkulatori
Pievienojiet Trigonometrijas Kalkulators savai vietnei