Matemaattiset Laskimet
Trigonometrinen Laskin
Laske helposti trigonometriset arvot Sin, Cos, Tan, Cot, Sec ja Csc ilmaisella online-laskimellamme!
Trigonometrinen laskin
Sisällysluettelo
| ◦Mikä on trigonometria? |
| ◦Mitkä ovat ensisijaiset tai perustrigonometriset funktiot? |
| ◦Mitä ovat käänteiset trigonometriset funktiot? |
| ◦Mihin trigonometriaa käytetään? |
| ◦Trigonometrian tosielämän sovellukset |
Mikä on trigonometria?
Trigonometria on matematiikan haara, joka käsittelee kolmion sivuja ja kulmia. Tämä aihe kattaa myös kulmien laskennassa käytettävät funktiot.
Mitkä ovat ensisijaiset tai perustrigonometriset funktiot?
Alla näet luettelon tärkeimmistä trigonometrisista funktioista, joita käytetään pääasiassa trigonometriaa käytettäessä.
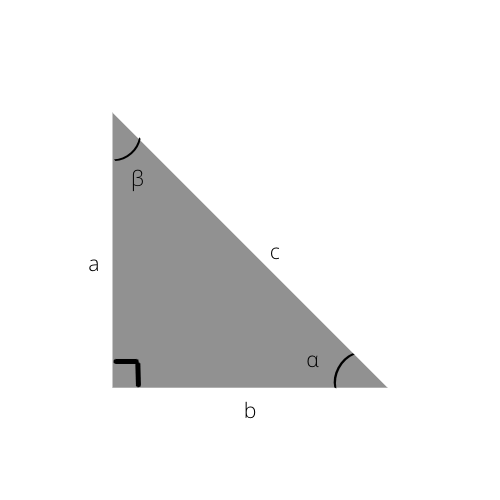
Esimerkki suorakulmaisesta kolmiosta. Tämän kuvan "α"-kulmaan viitataan seuraavissa kaavoissa.
1) Kulman sini
Kaava: sin α = vastakohta / hypotenuusa
Kulman sinin suhde suorakulmaisen kolmion yhteydessä on vastakohdan pituus jaettuna hypotenuusan pituudella.
2) Kulman kosini
Kaava: cos α = vierekkäinen / hypotenuusa
Kulman kosini suorakulmaisen kolmion yhteydessä lasketaan jakamalla viereisen pituus hypotenuusan pituudella.
3) Kulman tangentti
Kaava: tan α = sin α / cos α = vastakkainen / vierekkäinen
Kulman tangentti suorakulmaisen kolmion yhteydessä lasketaan jakamalla sini kosinilla. Tämä voidaan myös korvata jakamalla vastakohta viereisellä.
Muista myös trigonometrinen taulukko, kun käytät näitä toimintoja.
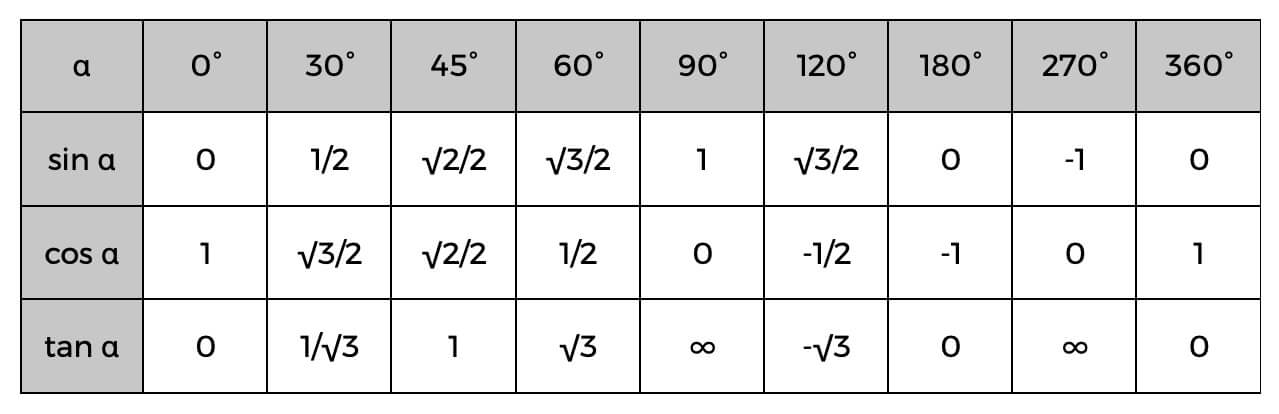
Trigonometrinen taulukko
Mitä ovat käänteiset trigonometriset funktiot?
Ensisijaisten trigonometristen funktioiden lisäksi on myös toinen joukko funktioita, joita ei käytetä ensimmäiseen luokkaan verrattuna. Näitä ovat sekantti (sec), kosekantti (csc) ja kotangentti (cot).
Mihin trigonometriaa käytetään?
Trigonometria liittyy kolmioihin, erityisesti suorakulmaisiin kolmioihin. Joten missä tahansa näet kolmion matematiikan maailman ulkopuolella, voit veikata, että trigonometria on hyödyllinen. Esimerkki tästä on trigonometristen laskelmien käyttö sellaisilla aloilla kuin arkkitehtuuri, tähtitiede ja kemiantekniikka.
Trigonometrian tosielämän sovellukset
Trigonometrian ilmeisen käytön lisäksi, joka on matematiikassa, trigonometriaa käytetään myös tosielämän tilanteissa ja aloilla.
1) Arkkitehtuuri ja suunnittelu
Ei ole liian kaukana ajatella trigonometristen funktioiden käyttöä arkkitehtuurissa. Näitä toimintoja käytetään enimmäkseen laskemaan diagonaalisen liitoksen pituus, joka yhdistää kaksi linjaa. Tätä käytetään laskettaessa katon kaltevuuden diagonaalipituutta, kun suunnitellaan kalteva katto. Sinun tarvitsee vain tietää katon korkeus ja pituus ja olet valmis!

2) Tähtitiede
Tähtitiede on tärkeä aihe, johon vanhat kulttuurit kiinnittivät enimmäkseen huomiota. Tästä puhuttaessa tulee luultavasti ensimmäisenä mieleen tähtikuviot ja niiden etäisyyden laskeminen toisistaan ja muista avaruuden kohteista, mikä on yksi tähtitieteen yksinkertaisimmista käyttötavoista. Toisin sanoen trigonometriaa voidaan käyttää laskemaan auringon ja maan etäisyyttä eri tähdistä. Tähtien etäisyys on tärkeä niiden tekijöiden laskemisessa tähtitieteen maailmassa.
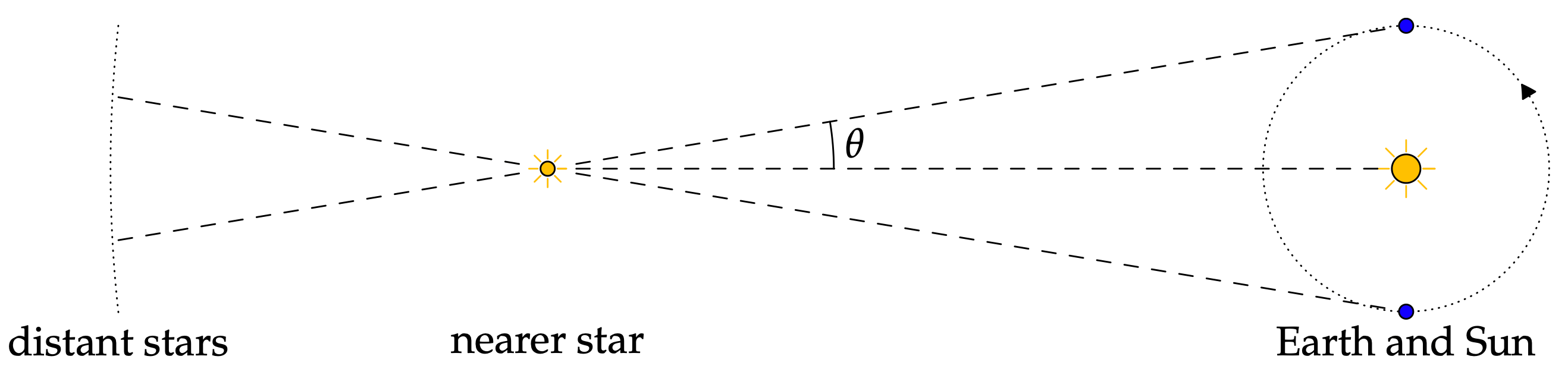
Katso tästä artikkelista lisätietoja tähtitiedestä ja sen suhteesta trigonometriaan:
3) Elektroniikka ja sähkötekniikka
Trigonometriaa käytetään elektroniikan ja sähkötekniikan matemaattisten ongelmien ratkaisemiseen, lähinnä mallin suunnittelussa. Toinen esimerkki tärkeydestä on esteettisten lisäysten tekeminen ja varmistaminen, etteivät ne häiritse mallin toimintaa.
Trigonometriset funktiot ovat kuitenkin erittäin hyödyllisiä piirien kanssa työskennellessä. Katso alla oleva visuaalinen esimerkki lisäesittelyä varten ja saadaksesi käsityksen siitä, kuinka trigonometria muuttuu piirilogiikaksi.
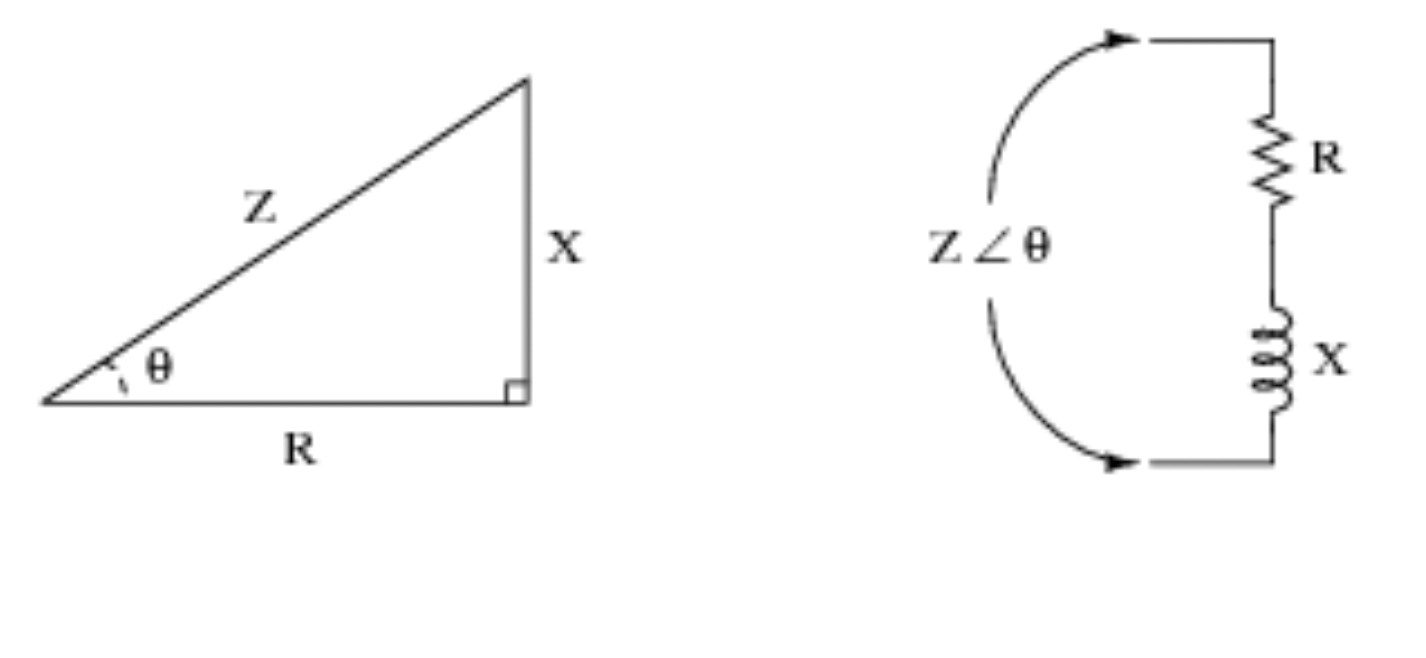
4) Seismologia
Seismologia tutkii maanjäristyksiä sekä maan läpi ja ympärillä liikkuvia seismisi aaltoja. Trigonometria helpottaa seismisen aallon kulkeman pysty- ja vaakamatkan laskemista.

5) Maanmittaus (maa- ja vesirakentaminen)
Maanmittaus on ollut ammatti, joka on ollut olemassa jo pitkään, ainakin niin kauan kuin historia osoittaa. Tämän tekee katsastaja, jonka tehtävänä on mitata maan pinnat tarkasti suuressa mittakaavassa. Olet ehkä jo arvannut trigonometrian käytön; pohjimmiltaan trigonometria tulee käyttöön, kun mittaajan on laskettava pituus, alueet ja suhteelliset kulmat maiseman kohteiden välillä.
Alla oleva esimerkki on hyvä visuaalinen osoitus siitä, mitä on aiemmin selitetty. Mittari laskee trigonometristen murtolukujen avulla oman etäisyyteensä vuoren huipulta tai mistä tahansa muualta valitsemastaan.

Artikkelin kirjoittaja
Parmis Kazemi
Parmis on sisällöntuottaja, jolla on intohimo kirjoittaa ja luoda uusia asioita. Hän on myös erittäin kiinnostunut tekniikasta ja nauttii uusien asioiden oppimisesta.
Trigonometrinen Laskin Suomi
Julkaistu: Fri Oct 29 2021
Luokassa Matemaattiset laskimet
Lisää Trigonometrinen Laskin omalle verkkosivustollesi