Matematické Kalkulačky
Kalkulačka Trigonometrie
Spočítejte si snadno trigonometrické hodnoty Sin, Cos, Tan, Cot, Sec a Csc pomocí naší bezplatné online kalkulačky!
Kalkulačka trigonometrie
Obsah
| ◦Co je to trigonometrie? |
| ◦Jaké jsou primární nebo základní goniometrické funkce? |
| ◦Co jsou to reciproké goniometrické funkce? |
| ◦K čemu se používá trigonometrie? |
| ◦Reálné aplikace trigonometrie |
Co je to trigonometrie?
Trigonometrie je odvětví matematiky zabývající se stranami a úhly v trojúhelníku. Tento předmět také pokrývá příslušné funkce používané pro výpočet úhlů.
Jaké jsou primární nebo základní goniometrické funkce?
Níže uvidíte seznam primárních goniometrických funkcí, které se používají hlavně při používání trigonometrie.
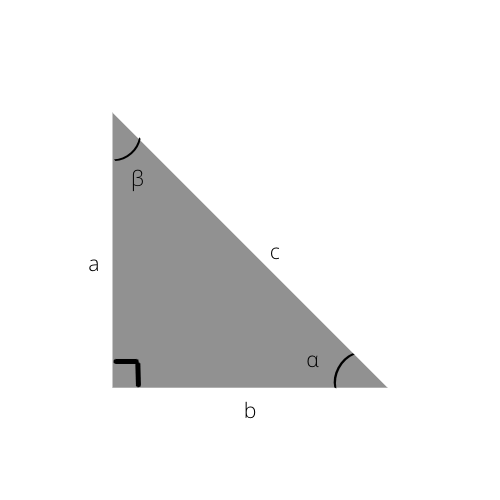
Příklad pravoúhlého trojúhelníku. Úhel "α" na tomto obrázku je uveden v následujících vzorcích.
1) Sinus úhlu
Vzorec: sin α = opak / přepona
Poměr sinusu úhlu v kontextu pravoúhlého trojúhelníku je délka protějšího dělená délkou přepony.
2) Kosinus úhlu
Vzorec: cos α = sousední / přepona
Kosinus úhlu v kontextu pravoúhlého trojúhelníku se vypočítá vydělením délky přilehlého bodu délkou přepony.
3) Tangenta úhlu
Vzorec: tan α = sin α / cos α = opačné / sousední
Tangenta úhlu v kontextu pravoúhlého trojúhelníku se vypočítá vydělením sinusu kosinusem. To lze také nahradit vydělením opaku sousedním.
Při používání těchto funkcí mějte také na paměti goniometrickou tabulku.
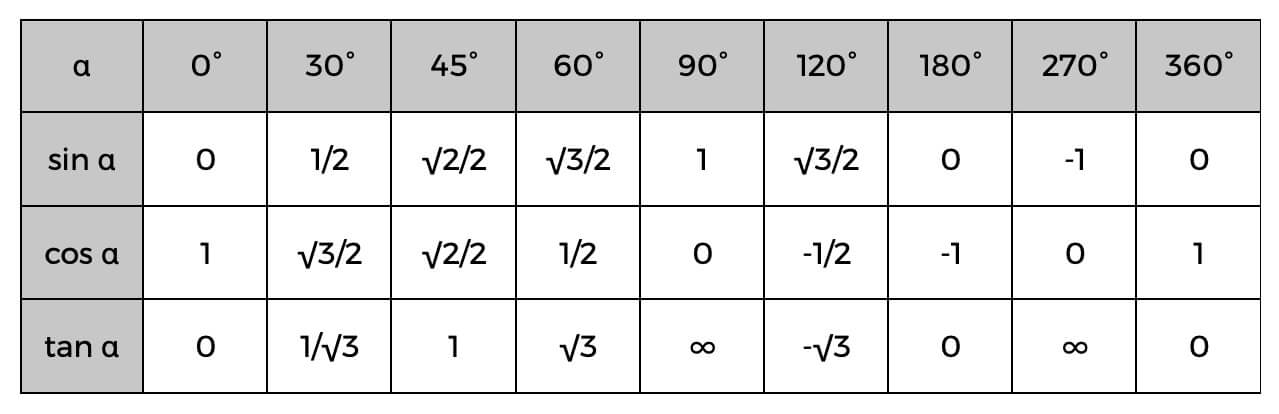
Trigonometrická tabulka
Co jsou to reciproké goniometrické funkce?
Kromě primárních goniometrických funkcí existuje také další sada funkcí, které nejsou tak používané ve srovnání s první kategorií. Patří mezi ně sečna (sec), kosekans (csc) a kotangens (cot).
K čemu se používá trigonometrie?
Trigonometrie souvisí s trojúhelníky, zejména pravoúhlými trojúhelníky. Takže, kdekoli uvidíte trojúhelník mimo matematický svět, vsadíte se, že trigonometrie je užitečná. Příkladem toho je použití trigonometrických výpočtů v oborech, jako je architektura, astronomie a chemické inženýrství.
Reálné aplikace trigonometrie
Kromě zřejmého použití trigonometrie, která je v matematice, se trigonometrie používá také v reálných situacích a polích.
1) Architektura a inženýrství
K zamyšlení nad využitím goniometrických funkcí v architektuře není příliš daleko. Tyto funkce se většinou používají k výpočtu délky diagonálního spojení, které spojuje dvě čáry. To se používá k výpočtu diagonální délky sklonu střechy při navrhování šikmé střechy. Stačí znát výšku a délku střechy a můžete vyrazit!

2) Astronomie
Astronomie je důležitým tématem, kterému staré kultury většinou věnovaly pozornost. Když o tom mluvíme, pravděpodobně jedna z prvních věcí, která vás napadne, jsou souhvězdí a výpočet jejich vzdálenosti od sebe navzájem a od ostatních objektů ve vesmíru, což je jedno z jednodušších použití astronomie. Jinými slovy, trigonometrie může být použita k výpočtu vzdálenosti Slunce a Země od různých hvězd. Vzdálenost hvězd je důležitá pro výpočet jejich faktorů ve světě astronomie.
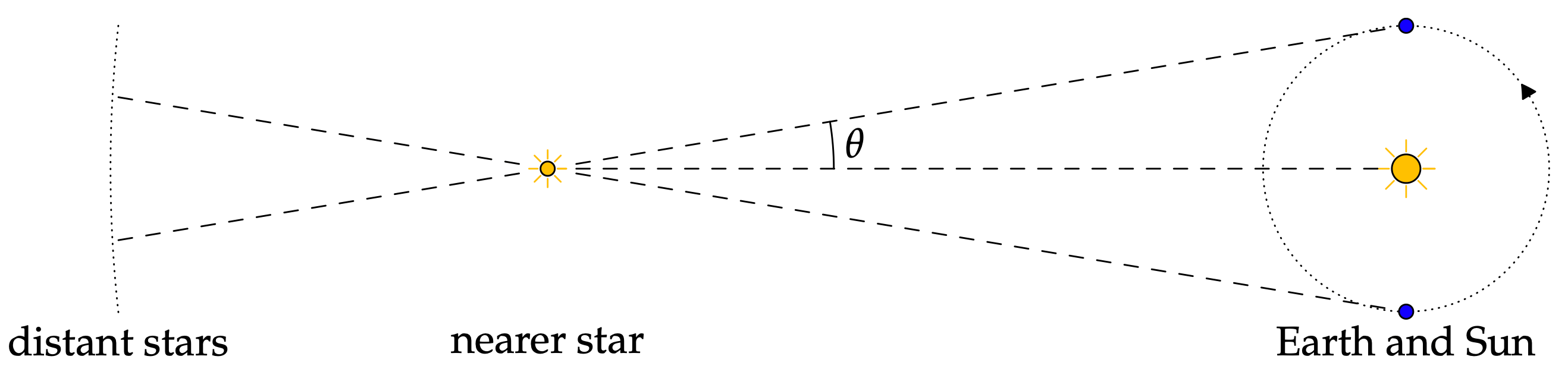
Další informace o astronomii a jejím vztahu k trigonometrii naleznete v tomto článku:
3) Elektronika a elektrotechnika
Trigonometrie se používá k řešení matematických úloh v elektronice a elektrotechnice, většinou při návrhu modelu. Dalším příkladem důležitosti je při vytváření estetických doplňků a zajištění toho, aby nenarušovaly funkci modelu.
Goniometrické funkce však přijdou velmi vhod při práci s obvody. Viz níže uvedený vizuální příklad pro další demonstraci a pro získání představy o tom, jak se trigonometrie převádí do logiky obvodu.
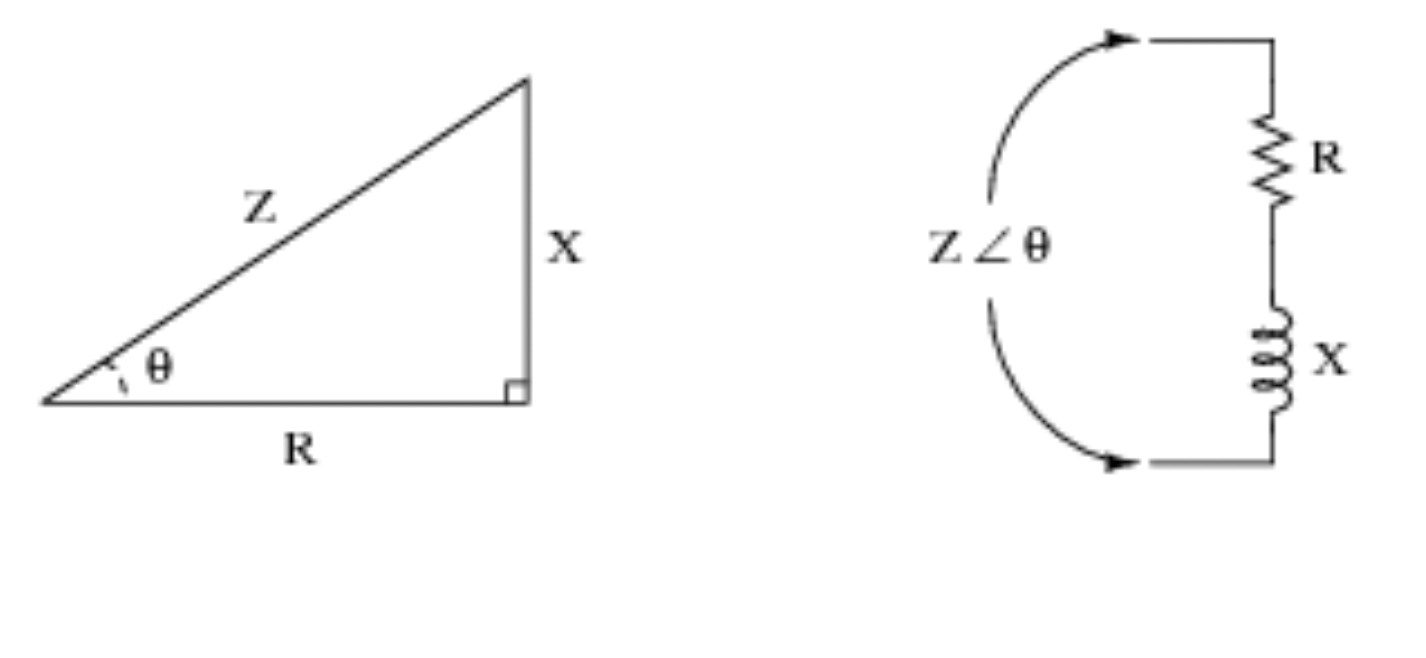
4) Seismologie
Seismologie je studium zemětřesení, stejně jako seismických vln, které se pohybují skrz a kolem Země. Trigonometrie přichází k usnadnění výpočtu vertikální a horizontální vzdálenosti, kterou seismická vlna urazí.

5) Zeměměřictví (stavební inženýrství)
Zeměměřictví je profese, která existuje již dlouhou dobu, alespoň tak dlouho, jak ukazuje zaznamenaná historie. Dělá to geodet, který má za úkol přesně měřit zemské povrchy ve velkém měřítku. Už jste možná uhodli použití trigonometrie; v zásadě trigonometrie přichází na řadu, když geodet potřebuje vypočítat délku, plochy a relativní úhly mezi objekty na krajině.
Níže uvedený příklad je dobrým vizuálním demonstrátorem toho, co bylo vysvětleno dříve. Geodet používá trigonometrické zlomky k výpočtu své vlastní vzdálenosti od vrcholu hory nebo odkudkoli jinde, které si vybere.

Autor článku
Parmis Kazemi
Parmis je tvůrce obsahu, který má vášeň pro psaní a vytváření nových věcí. Má také velký zájem o technologie a ráda se učí nové věci.
Kalkulačka Trigonometrie čeština
Zveřejněno: Fri Oct 29 2021
V kategorii Matematické kalkulačky
Přidejte Kalkulačka Trigonometrie na svůj vlastní web