Matematiniai Skaičiuotuvai
Trigonometrijos Skaičiuotuvas
Lengvai apskaičiuokite trigonometrines reikšmes Sin, Cos, Tan, Cot, Sec ir Csc su mūsų nemokama internetine skaičiuokle!
Trigonometrijos skaičiuotuvas
Turinys
Kas yra trigonometrija?
Trigonometrija yra matematikos šaka, nagrinėjanti trikampio kraštines ir kampus. Ši tema taip pat apima atitinkamas funkcijas, naudojamas skaičiuojant kampus.
Kokios yra pagrindinės arba pagrindinės trigonometrinės funkcijos?
Žemiau pamatysite pagrindinių trigonometrinių funkcijų, kurios dažniausiai naudojamos naudojant trigonometriją, sąrašą.
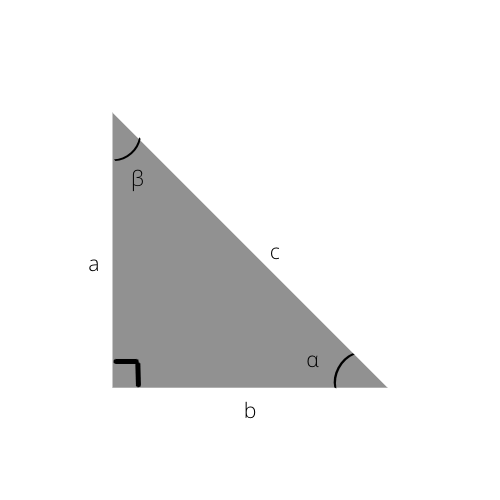
Stačiakampio trikampio pavyzdys. „α“ kampas šiame paveikslėlyje nurodytas šiose formulėse.
1) Kampo sinusas
Formulė: sin α = priešinga / hipotenuzė
Kampo sinuso santykis stačiakampio trikampio kontekste yra priešingo ilgis, padalytas iš hipotenuzės ilgio.
2) Kampo kosinusas
Formulė: cos α = gretimas / hipotenuzė
Kampo kosinusas stačiakampio trikampio kontekste apskaičiuojamas gretimo ilgį padalijus iš hipotenuzės ilgio.
3) Kampo liestinė
Formulė: tan α = sin α / cos α = priešingas / gretimas
Kampo liestinė stačiakampio trikampio kontekste apskaičiuojama sinusą padalijus iš kosinuso. Tai taip pat gali būti pakeista padalijus priešingą iš gretimo.
Be to, naudodamiesi šiomis funkcijomis, nepamirškite apie trigonometrinę lentelę.
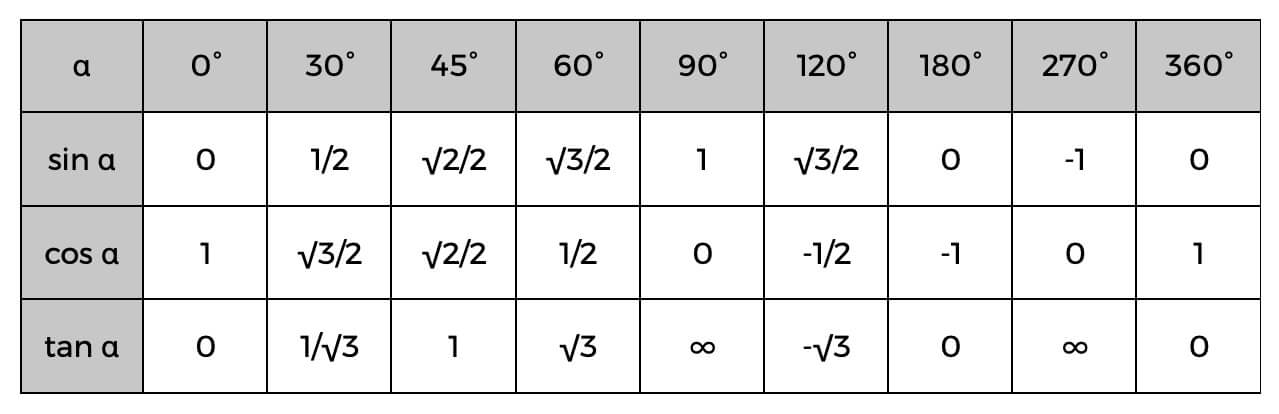
Trigonometrinė lentelė
Kas yra abipusės trigonometrinės funkcijos?
Be pirminių trigonometrinių funkcijų, yra ir kitas funkcijų rinkinys, kuris nėra taip naudojamas, lyginant su pirmąja kategorija. Tai apima sekantą (sec), kosekantą (csc) ir kotangentą (cot).
Kam naudojama trigonometrija?
Trigonometrija yra susijusi su trikampiais, ypač su stačiakampiais trikampiais. Taigi visur, kur matote trikampį už matematikos pasaulio ribų, galite lažintis, kad trigonometrija yra naudinga. To pavyzdys yra trigonometrinių skaičiavimų naudojimas tokiose srityse kaip architektūra, astronomija ir chemijos inžinerija.
Realūs trigonometrijos pritaikymai
Išskyrus akivaizdų trigonometrijos, kuri yra matematikoje, naudojimą, trigonometrija taip pat naudojama realiose situacijose ir laukuose.
1) Architektūra ir inžinerija
Nelabai toli reikia galvoti apie trigonometrinių funkcijų panaudojimą architektūroje. Šios funkcijos dažniausiai naudojamos apskaičiuojant dvi linijas jungiančios įstrižainės jungties ilgį. Tai naudojama stogo nuolydžio įstrižainės ilgiui apskaičiuoti projektuojant šlaitinį stogą. Jums tereikia žinoti stogo aukštį ir ilgį ir viskas!

2) Astronomija
Astronomija yra svarbi tema, kuriai senosios kultūros daugiausia dėmesio skyrė. Kalbant apie tai, tikriausiai vienas iš pirmųjų dalykų, kuris ateina į galvą, yra žvaigždynai ir jų atstumo vienas nuo kito ir kitų erdvėje objektų apskaičiavimas, o tai yra vienas iš paprastesnių astronomijos panaudojimo būdų. Kitaip tariant, trigonometrija gali būti naudojama saulės ir žemės atstumui nuo skirtingų žvaigždžių apskaičiuoti. Žvaigždžių atstumas yra svarbus skaičiuojant jų veiksnius astronomijos pasaulyje.
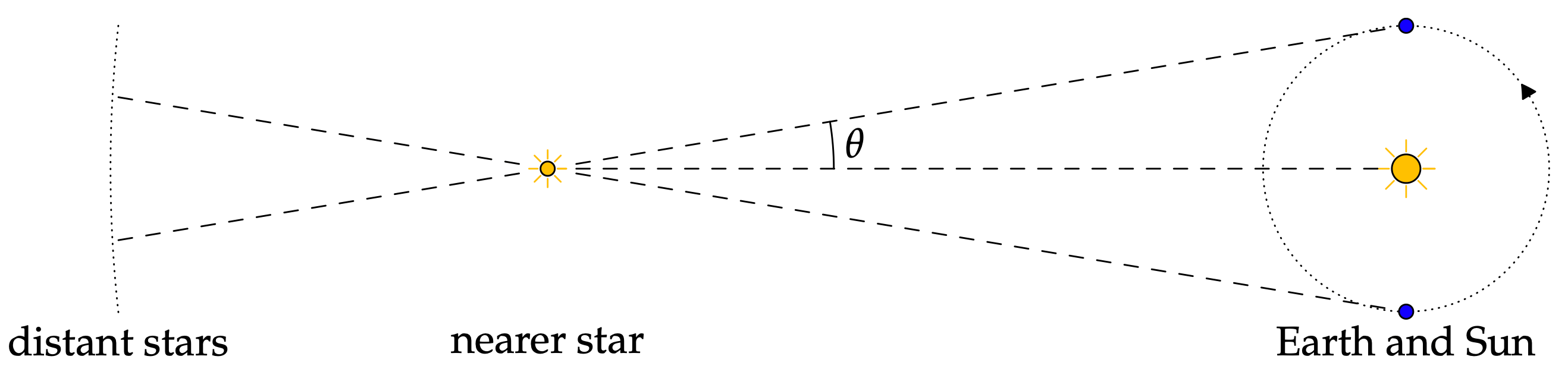
Daugiau informacijos apie astronomiją ir jos ryšį su trigonometrija rasite šiame straipsnyje:
3) Elektronika ir elektrotechnika
Trigonometrija naudojama sprendžiant matematines elektronikos ir elektrotechnikos problemas, dažniausiai kuriant modelį. Kitas svarbos pavyzdys – estetiniai papildymai ir užtikrinimas, kad jie netrikdytų modelio veikimo.
Tačiau trigonometrinės funkcijos labai praverčia dirbant su grandinėmis. Žiūrėkite toliau pateiktą vaizdinį pavyzdį, kad galėtumėte toliau demonstruoti ir suprasti, kaip trigonometrija paverčiama grandinės logika.
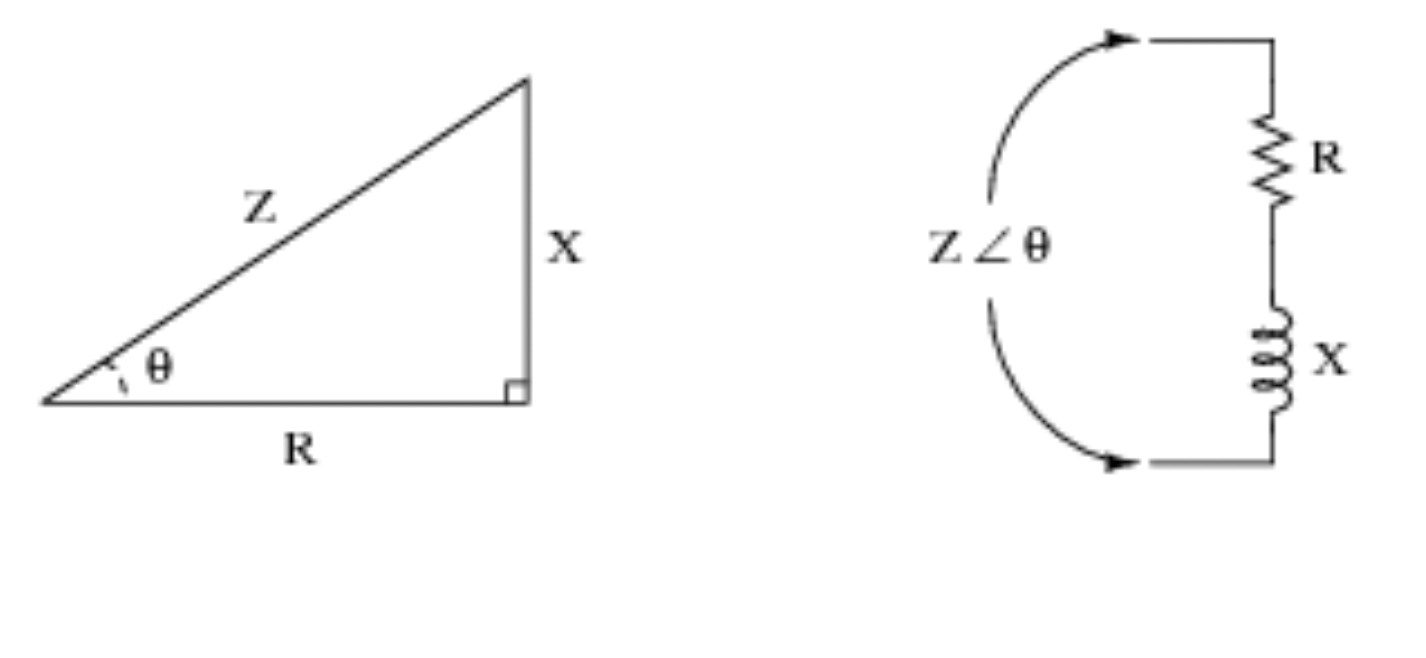
4) Seismologija
Seismologija yra žemės drebėjimų, taip pat seisminių bangų, judančių per žemę ir aplink ją, tyrimas. Trigonometrija padeda lengviau apskaičiuoti vertikalų ir horizontalų atstumą, kurį nukeliauja seisminė banga.

5) Žemės matavimas (statybinė inžinerija)
Geodezė buvo profesija, kuri gyvuoja jau seniai, bent jau tiek, kiek rodo įrašyta istorija. Tai atlieka matininkas, kurio užduotis yra tiksliai išmatuoti žemės paviršių dideliu mastu. Galbūt jau atspėjote apie trigonometrijos naudojimą; iš esmės trigonometrija atsiranda tada, kai matininkui reikia apskaičiuoti ilgį, plotus ir santykinius kampus tarp kraštovaizdžio objektų.
Toliau pateiktas pavyzdys yra geras vaizdinis to, kas buvo paaiškinta anksčiau, pavyzdys. Matininkas naudoja trigonometrines trupmenas, kad apskaičiuotų savo atstumą nuo kalno viršūnės arba nuo bet kurios kitos pasirinktos vietos.

Straipsnio autorius
Parmis Kazemi
Parmis yra turinio kūrėjas, kuris aistringai rašo ir kuria naujus dalykus. Ji taip pat labai domisi technologijomis ir mėgsta mokytis naujų dalykų.
Trigonometrijos Skaičiuotuvas Lietuvių
Paskelbta: Fri Oct 29 2021
Matematiniai skaičiuotuvai kategorijoje
Pridėkite Trigonometrijos Skaičiuotuvas prie savo svetainės