Matematiniai Skaičiuotuvai
Trikampio Hipotenuzės Skaičiuotuvas
Naudodami nemokamą matematikos skaičiuotuvą lengvai sužinokite hipotenuzą visų rūšių trikampiams!
Trikampio hipotenuzė iš dviejų pusių
Trikampio hipotenuzė iš vienos pusės ir ploto
Turinys
Kas yra trikampio hipotenuzė?
Hipotenuzė yra ilgiausia trikampio kraštinė. Ji taip pat yra priešinga nuo stačiojo kampo (90°) pusė.
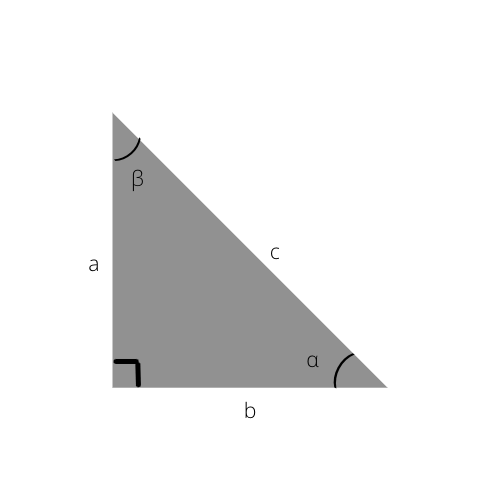
Šiame trikampyje hipotenuzė yra c.
Taip pat galite peržiūrėti šį Vikipedijos straipsnį:
Kodėl hipotenuzė yra ilgiausia trikampio kraštinė?
Pastebėję aukščiau pateiktą paveikslėlį ir kitus stačiuosius trikampius, pastebėsite, kad hipotenuzė visada yra ilgiausia visų stačiųjų trikampių kraštinė. Taip yra paprasčiausiai todėl, kad jis yra priešais didžiausią kampą, 90° kampą.
Tai taip pat galima įrodyti matematiškai naudojant Pitagoro teoremą:
a² + b² = c²
a² > b² , a² > c²
a > b , a > c
Kaip matote, aukščiau pateiktos operacijos rezultatas yra tas, kad „a“ (hipotenuzė) yra didesnė už kitas dvi puses.
Kaip apskaičiuoti trikampio hipotenuzę?
Tai galima padaryti 3 skirtingais būdais, atsižvelgiant į pateiktą informaciją, kuri gali būti toliau išvardytų veiksnių variantas:
a: priešinga pusė
b: gretimoje pusėje
c: hipotenuzės pusė
α: kampas tarp gretimos ir hipotenuzės
β: kampas tarp priešingos ir hipotenuzės
1) Dvi stačiojo trikampio kojos
Formula: c = √(a² + b²) or c² = a² + b²
Ši formulė pagrįsta Pitagoro teorema, kurią galima paprasčiausiai panaudoti paimant kvadratinę šaknį iš gretimų ir priešingų kvadratų sumos.
2) Kampas ir viena koja
Formula: c = a / sin(α) = b / sin(β)
Taip pat hipotenuzę galite apskaičiuoti naudodami sinusų dėsnį, kuris yra šios formulės pagrindas.
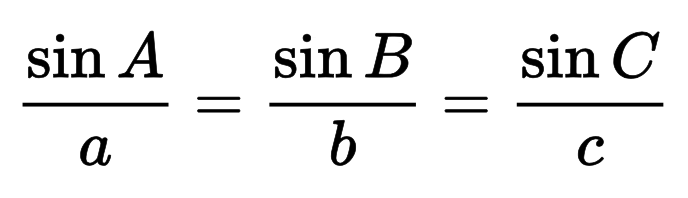
Bendrasis sinusų dėsnis
3) Plotas ir viena koja
Formula: c = √(a² + b²) = √(a² + (area _ 2 / a)²) = √((area _ 2 / b)² + b²)
Ši formulė pagrįsta formule, kurią naudojame trikampio plotui apskaičiuoti (a \* b / 2). Palyginti su kitais dviem, jis atrodo sudėtingesnis, tačiau vadovaujasi ta pačia logika kaip ir kiti du hipotenų skaičiavimo būdai.
Verta žinoti apie trigonometrines funkcijas
Jei vis dar norite sužinoti daugiau apie dešinįjį trikampį, peržiūrėkite šias trigonometrines funkcijas.
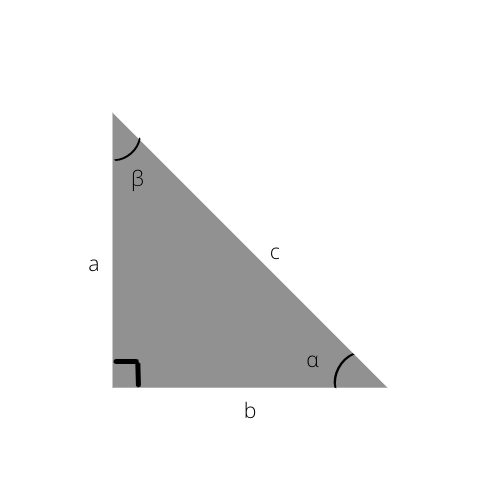
Žinodami tai, galite lengvai apskaičiuoti stačiojo trikampio kraštines arba net nustatyti kampus naudodami toliau pateiktą trigonometrinę lentelę.
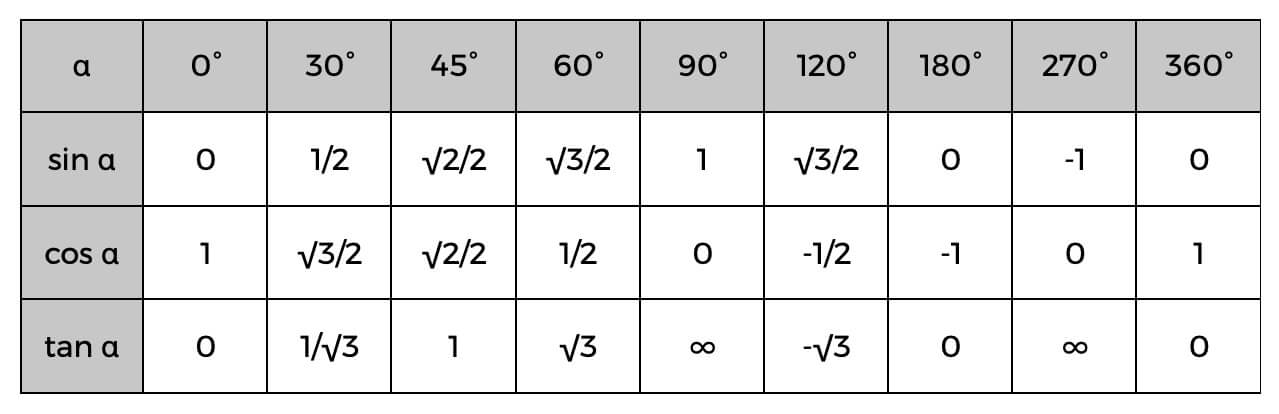
To pavyzdys gali būti tai, kad jūs jau žinote hipotenuzės ir gretimų reikšmę; galite lengvai rasti kampo kosinusą, tada patikrinkite aukščiau esančią lentelę, kad surastumėte tikslų kampą arba tiesiog įvertintumėte, koks jis galėtų būti. Jei alfa (α) kosinusas yra 0,5, tada žinome, kad kampas yra 60°.
Taip pat galite peržiūrėti šį Vikipedijos straipsnį:
Trikampių klasifikavimas pagal kraštines
1) Lygiakraščiai
Šis trikampis turi tris lygias kraštines. Dėl to visi kampai yra 60°.
Vaizdinis pavyzdys:

Lygiakraštis trikampis
2) Lygiašonis
Šiame trikampyje tik dvi kraštinės yra lygios.
Vaizdinis pavyzdys:

Lygiašonis trikampis
3) Skalena
Nė viena iš šio trikampio kraštinių nėra lygi.
Vizualus pavyzdys

Skaleninis trikampis
Trikampių klasifikavimas pagal kampus
1) Ūmus
Visi trys šio trikampio kampai yra mažesni nei 90°.
Vaizdinis pavyzdys:

Ūmus trikampis
2) Teisingai
Šis trikampis turi tik vieną 90° kampą, todėl kiti du yra mažesni nei 90°.
Kodėl?
α + β + γ = 180° & α = 90° → β + γ = 90° → β , γ < 90°
Vaizdinis pavyzdys:

Taisyklingas trikampis
3) Bukas
Šio trikampio vienas kampas yra didesnis nei 90°.
Vaizdinis pavyzdys:

Bukas trikampis
Įdomūs faktai apie trikampius
1 faktas:
Jei trikampio vidinis aukštis nubrėžtas, pradiniame trikampyje gauname du stačiuosius trikampius.
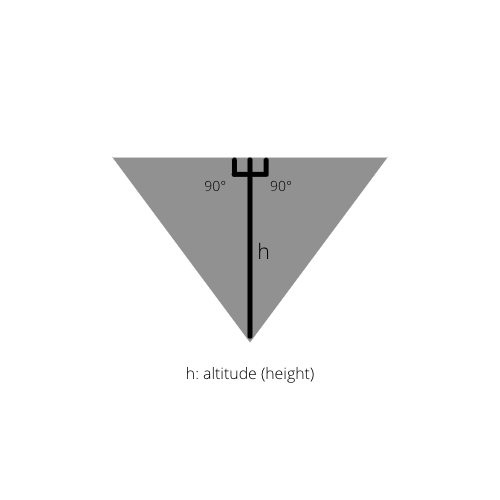
2 faktas:
Kaip žinome, bet kurio trikampio plotas (A) yra pusė aukščio, padauginto iš pagrindo (A = 1/2 _ b _ h). Šią formulę galima parašyti specialiu būdu lygiašoniam stačiakampiui trikampiui, nes jo plotas yra pusė kvadrato ploto.
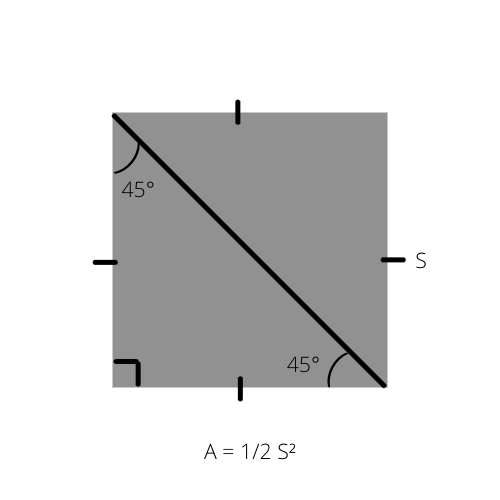
A yra trikampio plotas, o S - kvadrato kraštinė.
3 faktas:
Visų trijų trikampio kampų suma visada yra 180°. Tai pasakytina apie visus trikampius.
Straipsnio autorius
Parmis Kazemi
Parmis yra turinio kūrėjas, kuris aistringai rašo ir kuria naujus dalykus. Ji taip pat labai domisi technologijomis ir mėgsta mokytis naujų dalykų.
Trikampio Hipotenuzės Skaičiuotuvas Lietuvių
Paskelbta: Wed Oct 27 2021
Matematiniai skaičiuotuvai kategorijoje
Pridėkite Trikampio Hipotenuzės Skaičiuotuvas prie savo svetainės
Trikampio Hipotenuzės Skaičiuotuvas kitomis kalbomis
Calcolatrice Triangolo IpotenusaTriangle Hypotenuse CalculatorKalkulator Hipotenus SegitigaTriangel Hypotenusa RäknareKolmion Hypotenuusan LaskinTrekanthypotenuskalkulatorLommeregner For Trekant HypotenusDriehoek Hypotenusa RekenmachineKalkulator Przeciwprostokątnej TrójkątaMáy Tính Cạnh Huyền Tam Giác