Математические Калькуляторы
Калькулятор Гипотенузы Треугольника
Найдите гипотенузу для всех видов треугольников с помощью нашего бесплатного математического калькулятора!
Гипотенуза треугольника с двух сторон
Гипотенуза треугольника по одной стороне и площади
Оглавление
Что такое гипотенуза треугольника?
Гипотенуза - это самая длинная сторона треугольника. Это также сторона, противоположная прямому углу (90 °).
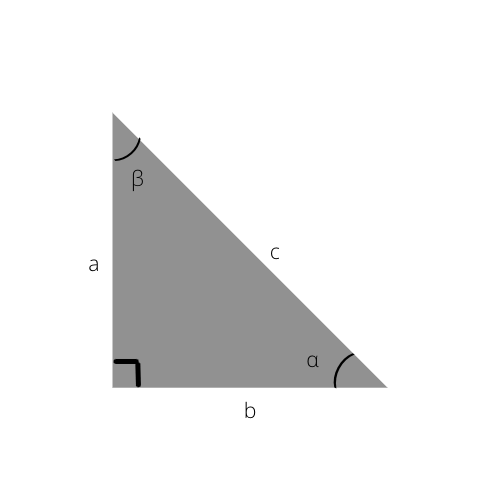
Гипотенуза в этом треугольнике равна c.
Вы также можете прочитать эту статью в Википедии:
Почему гипотенуза - самая длинная сторона треугольника?
Изучив рисунок выше и другие прямоугольные треугольники, вы заметите, что гипотенуза всегда является самой длинной стороной всех прямоугольных треугольников. Это просто потому, что он расположен напротив самого большого угла, угла 90 °.
это также можно доказать математически с помощью теоремы Пифагора:
a² + b² = c²
a² > b² , a² > c²
a > b , a > c
Как видите, результат вышеописанной операции состоит в том, что «a» (гипотенуза) больше двух других сторон.
Как рассчитать гипотенузу треугольника?
Это можно сделать 3 разными способами, в зависимости от предоставленной информации, которая может быть вариацией факторов, перечисленных ниже:
а: противоположная сторона
b: прилегающая сторона
c: сторона гипотенузы
α: угол между соседней и гипотенузой
β: угол между противоположной стороной и гипотенузой
1) Две ножки прямоугольного треугольника
Formula: c = √(a² + b²) or c² = a² + b²
Эта формула основана на теореме Пифагора, которую можно просто использовать, извлекая квадратный корень из суммы квадратов смежных и противоположных чисел.
2) Угол и одна нога
Formula: c = a / sin(α) = b / sin(β)
Вы также можете вычислить гипотенузу, используя закон синусов, который является основой этой формулы.
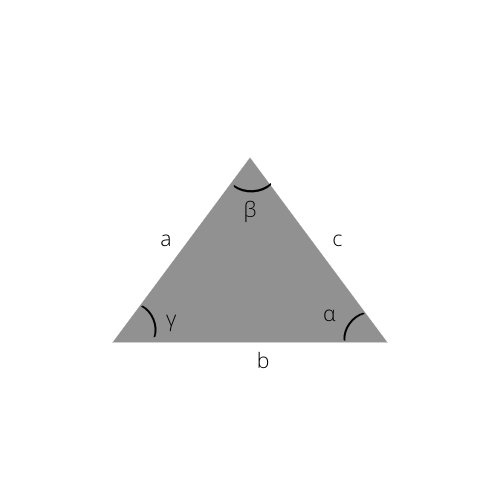
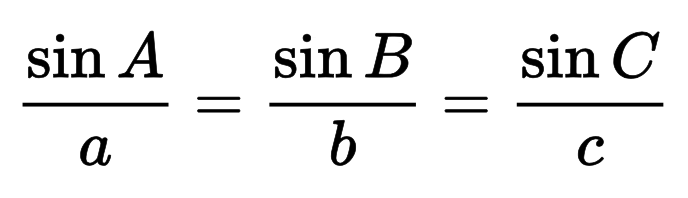
Общий закон синусов
3) Площадь и одна нога
Formula: c = √(a² + b²) = √(a² + (area _ 2 / a)²) = √((area _ 2 / b)² + b²)
Эта формула основана на формуле, которую мы используем для вычисления площади треугольника (a \ * b / 2). По сравнению с двумя другими он выглядит более сложным, однако он следует той же логике, что и два других способа вычисления гипотенузы.
Полезно знать о тригонометрических функциях
Если вы все еще хотите узнать больше о прямоугольном треугольнике, ознакомьтесь с этими тригонометрическими функциями.
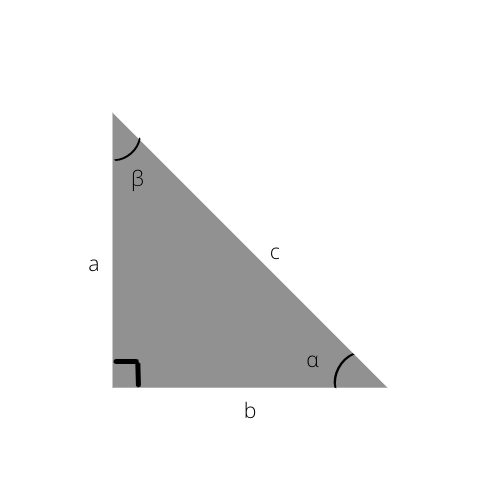
Зная их, вы можете легко вычислить стороны прямоугольного треугольника или даже определить углы, используя приведенную ниже тригонометрическую таблицу.
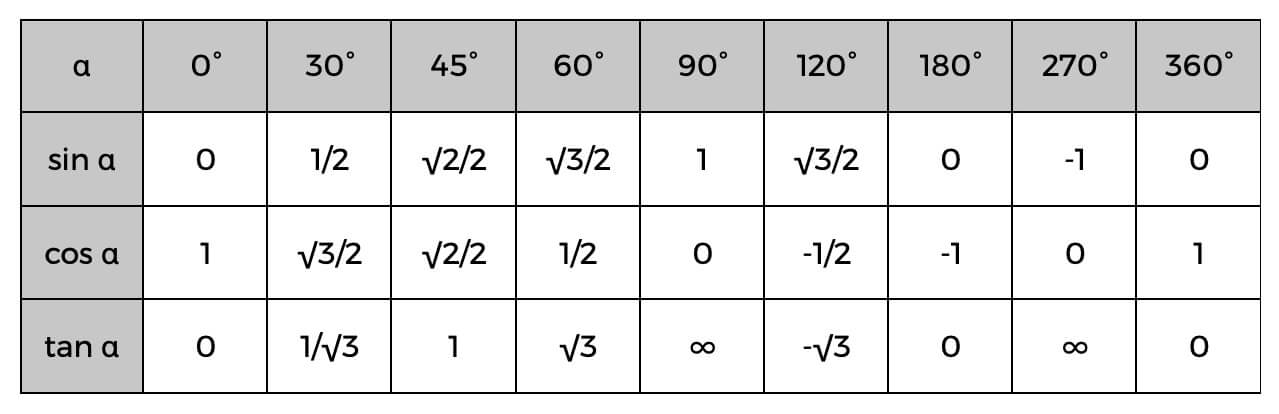
Примером этого может быть то, что вы уже знаете значение гипотенузы и смежной; вы можете легко найти косинус угла, а затем проверить таблицу выше, чтобы найти точный угол или просто приблизительную оценку того, каким он может быть. Если косинус альфа (α) равен 0,5, то мы знаем, что угол равен 60 °.
Вы также можете прочитать эту статью в Википедии:
Классификация треугольников по сторонам
1) Равносторонний
У этого треугольника три равные стороны. В результате все углы составляют 60 °.
Наглядный пример:

Равносторонний треугольник
2) Равнобедренная
В этом треугольнике равны только две стороны.
Наглядный пример:

Равнобедренный треугольник
3) Скален
В этом треугольнике все стороны не равны.
Наглядный пример

Неравносторонний треугольник
Классификация треугольников по углам
1) острый
Все три угла в этом треугольнике меньше 90 °.
Наглядный пример:

Острый треугольник
2) Право
У этого треугольника только один угол 90 °, в результате два других меньше 90 °.
Почему?
α + β + γ = 180° & α = 90° → β + γ = 90° → β , γ < 90°
Наглядный пример:

Прямоугольный треугольник
3) Тупой
У этого треугольника один угол больше 90 °.
Наглядный пример:

Тупой треугольник
Интересные факты о треугольниках
Факт 1:
Если нарисовать внутреннюю высоту треугольника, мы получим два прямоугольных треугольника в исходном треугольнике.
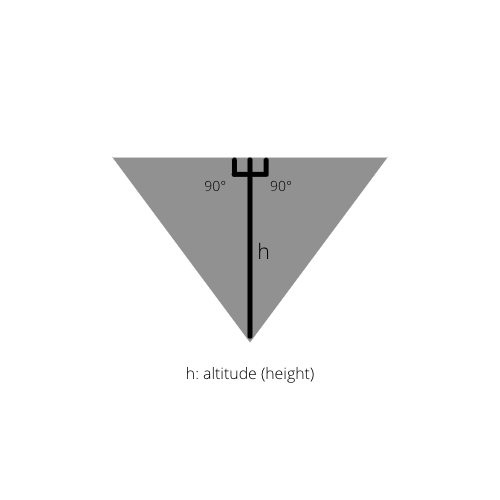
Факт 2:
Как мы знаем, площадь любого треугольника (A) равна половине высоты, умноженной на основание (A = 1/2 _ b _ h). Эта формула может быть записана особым образом для равнобедренного прямоугольного треугольника, поскольку его площадь составляет половину площади квадрата.
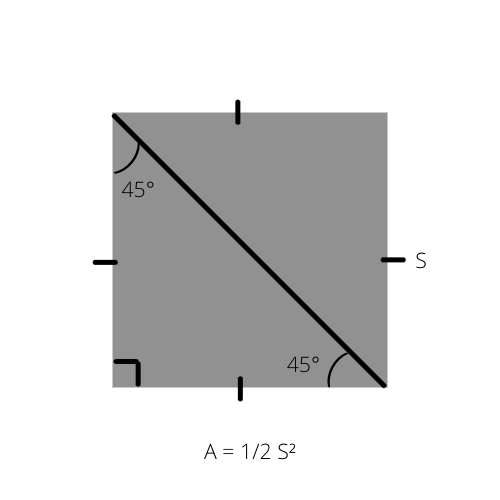
A - это площадь треугольника, а S - сторона квадрата.
Факт 3:
Сумма всех трех углов треугольника всегда составляет 180 °. Это верно для всех треугольников.
Автор статьи
Parmis Kazemi
Пармис - создатель контента, который любит писать и создавать новые вещи. Она также очень интересуется технологиями и любит узнавать что-то новое.
Калькулятор Гипотенузы Треугольника русский
Опубликовано: Wed Oct 27 2021
В категории Математические калькуляторы
Добавьте Калькулятор Гипотенузы Треугольника на свой сайт