Máy Tính Toán Học
Máy Tính Cạnh Huyền Tam Giác
Dễ dàng tìm ra cạnh huyền cho tất cả các loại tam giác bằng máy tính toán miễn phí của chúng tôi!
Cạnh huyền tam giác bằng hai cạnh
Cạnh huyền tam giác bằng một cạnh và diện tích
Mục lục
Cạnh huyền của một tam giác là gì?
Cạnh huyền là cạnh dài nhất của một tam giác. Nó cũng là mặt đối diện với góc vuông (90 °).
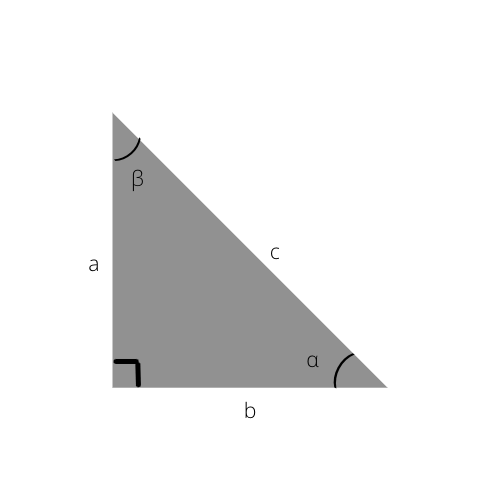
Cạnh huyền là c trong tam giác này.
Bạn cũng có thể xem bài viết Wikipedia này:
Tại sao cạnh huyền là cạnh dài nhất của tam giác?
Sau khi quan sát hình trên và các hình tam giác vuông khác, bạn sẽ nhận thấy cạnh huyền luôn là cạnh dài nhất của tất cả các hình tam giác vuông. Điều này đơn giản là vì nó nằm đối diện với góc lớn nhất, góc 90 °.
điều này cũng có thể được chứng minh bằng toán học bằng cách sử dụng Định lý Pitago:
a² + b² = c²
a² > b² , a² > c²
a > b , a > c
Như bạn thấy, kết quả của phép toán trên là "a" (cạnh huyền) lớn hơn hai cạnh còn lại.
Làm thế nào để tính cạnh huyền của một tam giác?
Điều này có thể được thực hiện theo 3 cách khác nhau, tùy thuộc vào thông tin đã cho có thể là biến thể của các yếu tố được liệt kê dưới đây:
a: phía đối diện
b: cạnh bên
c: cạnh huyền
α: góc giữa cạnh huyền và cạnh huyền
β: góc giữa đối diện và cạnh huyền
1) Hai chân tam giác vuông
Formula: c = √(a² + b²) or c² = a² + b²
Công thức này dựa trên định lý Pitago có thể được sử dụng một cách đơn giản bằng cách lấy căn bậc hai của tổng các bình phương của kề và đối diện.
2) Góc và một chân
Formula: c = a / sin(α) = b / sin(β)
Bạn cũng có thể tính toán cạnh huyền bằng cách sử dụng luật sin, đây là cơ sở của công thức này.
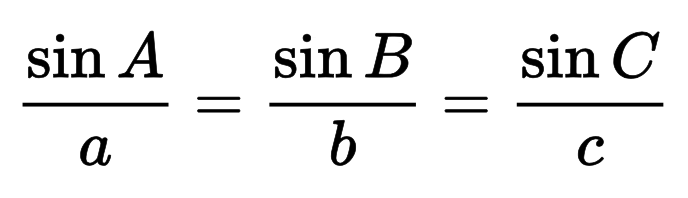
Quy luật chung của sin
3) Khu vực và một chân
Formula: c = √(a² + b²) = √(a² + (area _ 2 / a)²) = √((area _ 2 / b)² + b²)
Công thức này dựa trên công thức chúng tôi sử dụng để tính diện tích của một tam giác (a \ * b / 2). Tuy nhiên, so với hai cách kia, nó có vẻ phức tạp hơn, nó tuân theo cùng một logic như hai cách tính cạnh huyền còn lại.
Điều cần biết về các hàm lượng giác
Nếu bạn vẫn muốn biết thêm về tam giác vuông, hãy xem các Hàm lượng giác này.
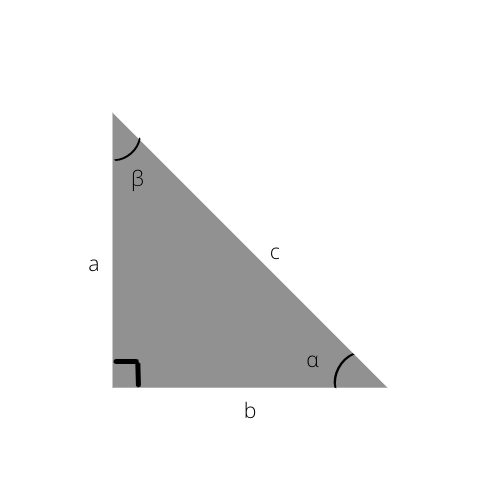
Biết được những điều này, bạn có thể dễ dàng tính các cạnh của tam giác vuông, hoặc thậm chí xác định các góc bằng cách sử dụng bảng lượng giác dưới đây.
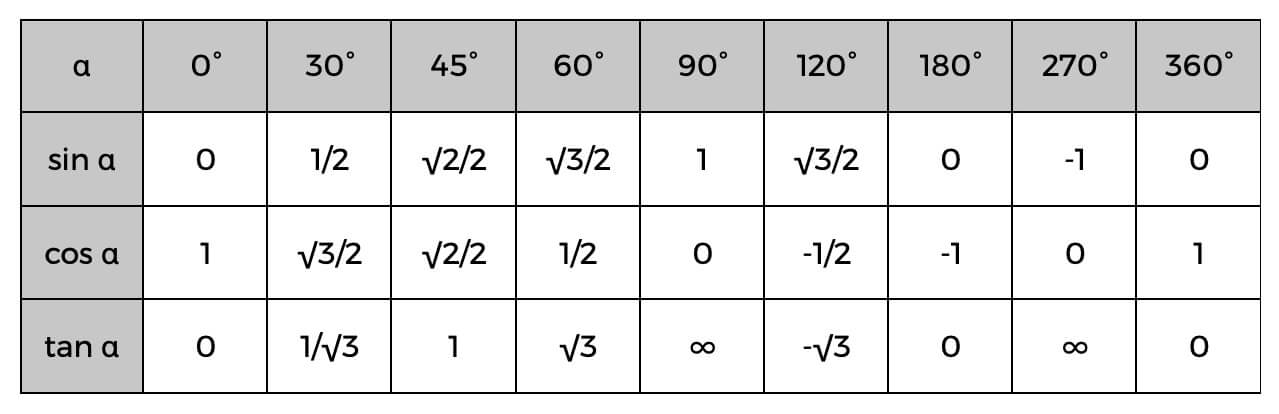
Một ví dụ về điều này có thể là bạn đã biết giá trị của cạnh huyền và cạnh kề; bạn có thể dễ dàng tìm ra cosin của góc, sau đó kiểm tra bảng trên để tìm góc chính xác hoặc chỉ là ước tính của nó có thể là gì. Nếu cosin của alpha (α) là 0,5, thì chúng ta biết rằng góc là 60 °.
Bạn cũng có thể xem bài viết Wikipedia này:
Phân loại hình tam giác dựa trên các cạnh
1) Bằng nhau
Tam giác này có ba cạnh bằng nhau. Điều này dẫn đến tất cả các góc đều là 60 °.
Ví dụ trực quan:

Tam giác đều
2) Isosceles
Trong tam giác này chỉ có hai cạnh bằng nhau.
Ví dụ trực quan:

Tam giác cân
3) Scalene
Không có cạnh nào bằng nhau trong tam giác này.
Ví dụ trực quan

Tam giác Scalene
Phân loại tam giác dựa trên các góc
1) Cấp tính
Cả ba góc trong tam giác này đều nhỏ hơn 90 °.
Ví dụ trực quan:

Tam giác nhọn
2) Đúng
Hình tam giác này chỉ có một góc 90 °, dẫn đến hai hình còn lại nhỏ hơn 90 °.
Tại sao?
α + β + γ = 180° & α = 90° → β + γ = 90° → β , γ < 90°
Ví dụ trực quan:

Tam giác vuông
3) Nghĩa vụ
Tam giác này có một góc lớn hơn 90 °.
Ví dụ trực quan:

Hình tam giác
Sự thật thú vị về hình tam giác
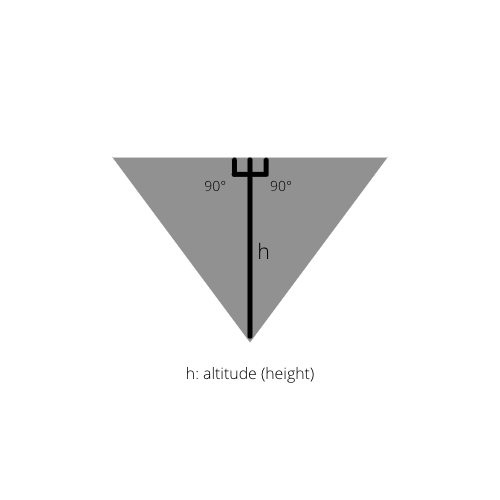
Sự thật 1:
Nếu vẽ đường cao trong của tam giác, ta được hai tam giác vuông trong tam giác ban đầu.
Sự thật 2:
Như chúng ta đã biết, diện tích của tam giác (A) bất kỳ là nửa chiều cao nhân với đáy (A = 1/2 _ b _ h). Công thức này có thể được viết theo một cách đặc biệt cho tam giác vuông cân vì diện tích của nó bằng một nửa diện tích hình vuông.
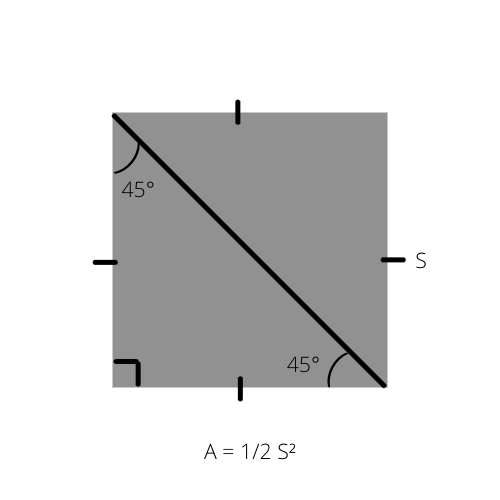
A là diện tích của tam giác và S là cạnh của hình vuông.
Sự thật 3:
Tổng cả ba góc của một tam giác luôn bằng 180 °. Điều này đúng với tất cả các hình tam giác.
Tác giả bài viết
Parmis Kazemi
Parmis là một người sáng tạo nội dung có niềm đam mê viết và tạo ra những thứ mới. Cô ấy cũng rất quan tâm đến công nghệ và thích học hỏi những điều mới.
Máy Tính Cạnh Huyền Tam Giác Tiếng Việt
Được phát hành: Wed Oct 27 2021
Trong danh mục Máy tính toán học
Thêm Máy Tính Cạnh Huyền Tam Giác vào trang web của riêng bạn