Mathematische Taschenrechner
Dreieck Hypotenuse Rechner
Finden Sie die Hypotenuse für alle Arten von Dreiecken ganz einfach mit unserem kostenlosen Mathematikrechner heraus!
Dreieckshypotenuse von zwei Seiten
Dreieckshypotenuse an einer Seite und Fläche
Inhaltsverzeichnis
Was ist die Hypotenuse eines Dreiecks?
Die Hypotenuse ist die längste Seite eines Dreiecks. Es ist auch die dem rechten Winkel (90°) gegenüberliegende Seite.
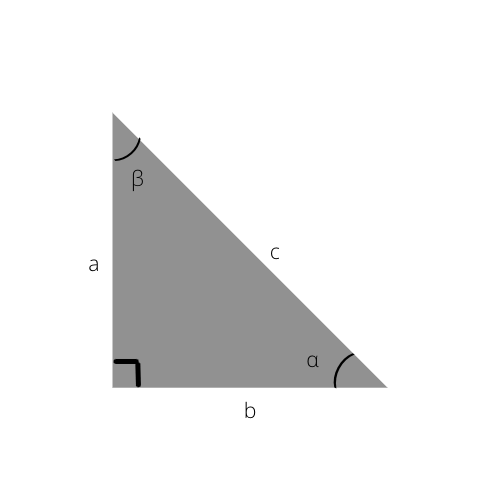
Die Hypotenuse ist in diesem Dreieck c.
Sie können auch diesen Wikipedia-Artikel lesen:
Warum ist die Hypotenuse die längste Seite des Dreiecks?
Nachdem Sie das obige Bild und andere rechtwinklige Dreiecke betrachtet haben, werden Sie feststellen, dass die Hypotenuse immer die längste Seite aller rechtwinkligen Dreiecke ist. Dies liegt einfach daran, dass er dem größten Winkel, dem 90°-Winkel, gegenüberliegt.
dies kann auch mathematisch mit dem Satz des Pythagoras bewiesen werden:
a² + b² = c²
a² > b² , a² > c²
a > b , a > c
Wie Sie sehen, ist das Ergebnis der obigen Operation, dass "a" (die Hypotenuse) größer ist als die anderen beiden Seiten.
Wie berechnet man die Hypotenuse eines Dreiecks?
Dies kann auf 3 verschiedene Arten erfolgen, abhängig von den gegebenen Informationen, die eine Variation der unten aufgeführten Faktoren sein können:
a: gegenüberliegende Seite
b: angrenzende Seite
c: Hypotenusenseite
α: Winkel zwischen Nachbar und Hypotenuse
β: Winkel zwischen Gegenstück und Hypotenuse
1) Zwei rechtwinklige Dreiecksbeine
Formula: c = √(a² + b²) or c² = a² + b²
Diese Formel basiert auf dem Satz des Pythagoras, der einfach verwendet werden kann, indem man eine Quadratwurzel aus der Summe der Quadrate des benachbarten und des Gegenteils zieht.
2) Winkel und ein Bein
Formula: c = a / sin(α) = b / sin(β)
Sie können die Hypotenuse auch berechnen, indem Sie das Sinusgesetz verwenden, das die Grundlage dieser Formel ist.
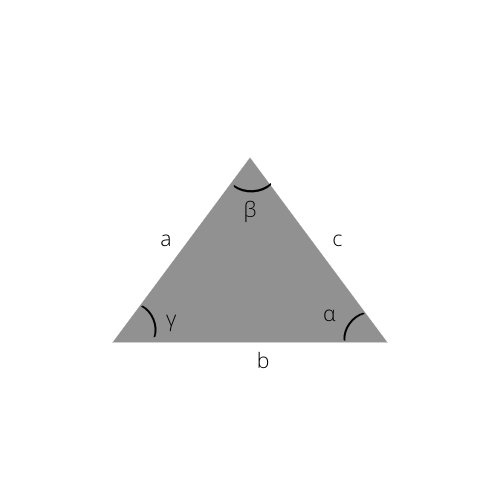
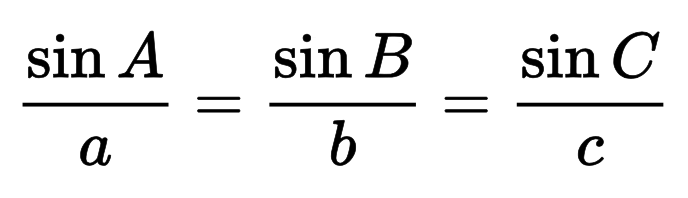
Das allgemeine Sinusgesetz
3) Bereich und ein Bein
Formula: c = √(a² + b²) = √(a² + (area _ 2 / a)²) = √((area _ 2 / b)² + b²)
Diese Formel basiert auf der Formel, mit der wir die Fläche eines Dreiecks berechnen (a \* b / 2). Im Vergleich zu den beiden anderen sieht es komplizierter aus, folgt aber der gleichen Logik wie die anderen beiden Methoden zur Berechnung von Hypotenusen.
Wissenswertes über trigonometrische Funktionen
Wenn Sie immer noch mehr über das rechtwinklige Dreieck wissen möchten, sehen Sie sich diese trigonometrischen Funktionen an.
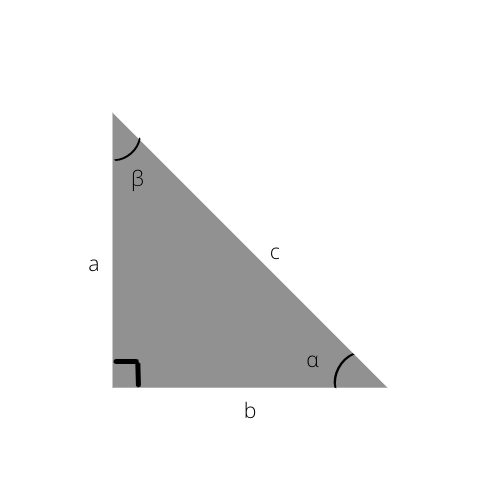
Wenn Sie diese kennen, können Sie die Seiten des rechtwinkligen Dreiecks leicht berechnen oder sogar die Winkel mithilfe der folgenden trigonometrischen Tabelle bestimmen.
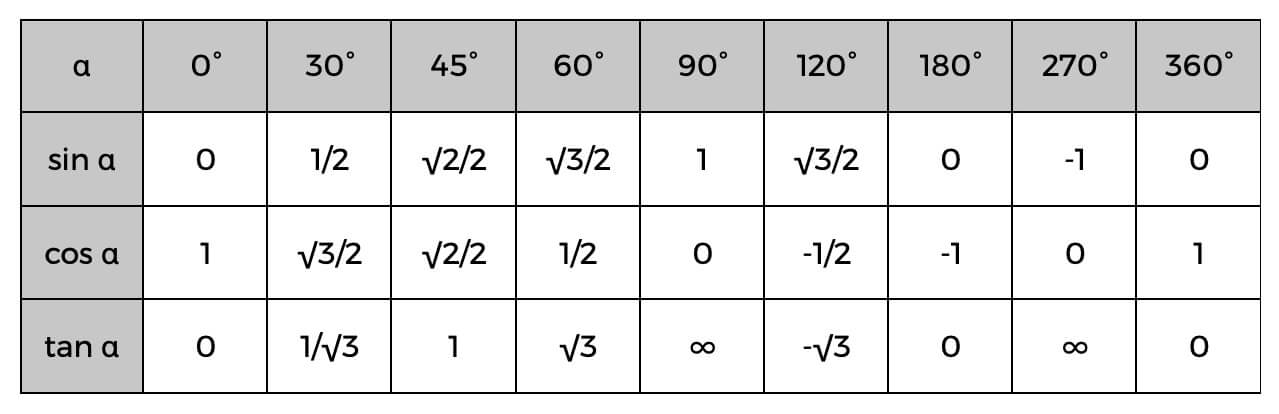
Ein Beispiel dafür kann sein, dass Sie den Wert der Hypotenuse und der angrenzenden bereits kennen; Sie können den Kosinus des Winkels leicht ermitteln und dann die obige Tabelle überprüfen, um den genauen Winkel zu finden oder nur eine Schätzung dessen, was er sein könnte. Wenn der Kosinus von Alpha (α) 0,5 beträgt, wissen wir, dass der Winkel 60° beträgt.
Sie können auch diesen Wikipedia-Artikel lesen:
Klassifizierung von Dreiecken nach den Seiten
1) Gleichseitig
Dieses Dreieck hat drei gleiche Seiten. Dies führt dazu, dass alle Winkel 60° betragen.
Visuelles Beispiel:

Gleichseitiges Dreieck
2) Gleichschenklig
In diesem Dreieck sind nur zwei Seiten gleich.
Visuelles Beispiel:

Gleichschenkligen Dreiecks
3) Schuppen
Keine der Seiten ist in diesem Dreieck gleich.
Visuelles Beispiel

Ungleichseitiges Dreieck
Klassifizierung von Dreiecken anhand der Winkel
1) Akut
Alle drei Winkel in diesem Dreieck sind kleiner als 90°.
Visuelles Beispiel:

Spitzwinkliges Dreieck
2) Richtig
Dieses Dreieck hat nur einen 90°-Winkel, was dazu führt, dass die anderen beiden kleiner als 90° sind.
Wieso den?
α + β + γ = 180° & α = 90° → β + γ = 90° → β , γ < 90°
Visuelles Beispiel:

Rechtwinkliges Dreieck
3) Stumpf
Dieses Dreieck hat einen Winkel, der größer als 90° ist.
Visuelles Beispiel:

Stumpfes Dreieck
Wissenswertes über Dreiecke
Fakt 1:
Wenn die innere Höhe des Dreiecks gezeichnet wird, erhalten wir zwei rechtwinklige Dreiecke im ursprünglichen Dreieck.
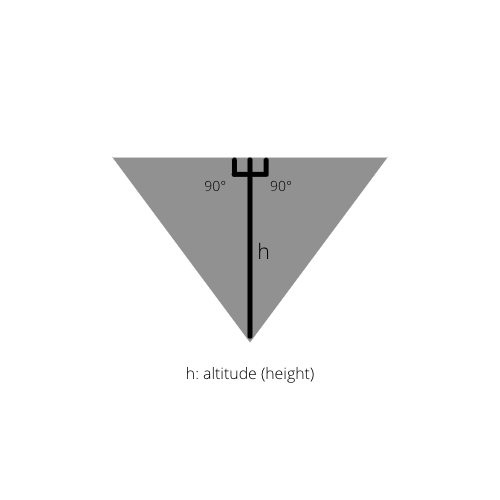
Fakt 2:
Wie wir wissen, ist die Fläche jedes Dreiecks (A) die Hälfte der Höhe multipliziert mit der Grundfläche (A = 1/2 _ b _ h). Diese Formel kann für das gleichschenklige rechtwinklige Dreieck in besonderer Weise geschrieben werden, da seine Fläche die Hälfte der Fläche eines Quadrats beträgt.
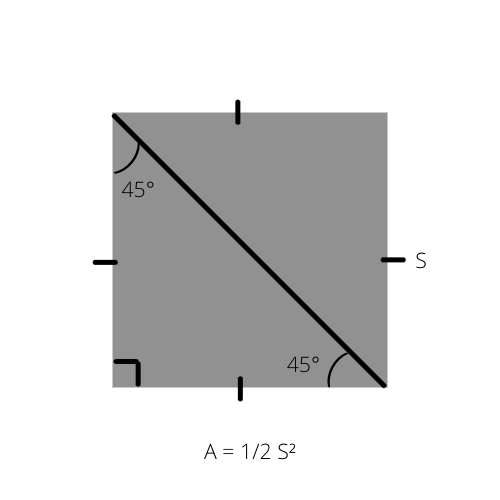
A ist die Fläche des Dreiecks und S die Seite des Quadrats.
Fakt 3:
Die Summe aller drei Winkel eines Dreiecks beträgt immer 180°. Dies gilt für alle Dreiecke.
Autor des Artikels
Parmis Kazemi
Parmis ist ein Content Creator, der eine Leidenschaft für das Schreiben und Erschaffen neuer Dinge hat. Außerdem interessiert sie sich sehr für Technik und lernt gerne Neues.
Dreieck Hypotenuse Rechner Deutsch
Veröffentlicht: Wed Oct 27 2021
In Kategorie Mathematische Taschenrechner
Dreieck Hypotenuse Rechner zu Ihrer eigenen Website hinzufügen