Matematiske Kalkulatorer
Trekanthypotenuskalkulator
Finn ut hypotenusen for alle slags trekanter enkelt med vår gratis matematikkkalkulator!
Triangelhypotenusa ved to sider
Trekant hypotenusa ved én side og areal
Innholdsfortegnelse
Hva er hypotenusen til en trekant?
Hypotenusen er den lengste siden av en trekant. Det er også siden motsatt fra rett vinkel (90°).
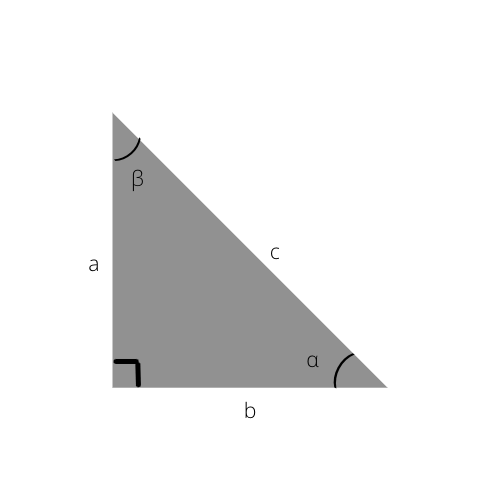
Hypotenusen er c i denne trekanten.
Du kan også sjekke ut denne Wikipedia-artikkelen:
Hvorfor er hypotenusen den lengste siden av trekanten?
Etter å ha observert bildet over, og andre rette trekanter, vil du legge merke til at hypotenusen alltid er den lengste siden av alle de rette trekantene. Dette er ganske enkelt fordi den er plassert motsatt av den største vinkelen, 90°-vinkelen.
dette kan også bevises matematisk ved å bruke Pythagoras teorem:
a² + b² = c²
a² > b² , a² > c²
a > b , a > c
Som du ser, er resultatet av operasjonen ovenfor at "a" (hypotenusen) er større enn de to andre sidene.
Hvordan beregne hypotenusen til en trekant?
Dette kan gjøres på 3 forskjellige måter, avhengig av den gitte informasjonen som kan være en variasjon av faktorene som er oppført nedenfor:
a: motsatt side
b: tilstøtende side
c: hypotenussiden
α: vinkel mellom den tilstøtende og hypotenusen
β: vinkel mellom motsatt og hypotenusen
1) To rettvinklede trekantbein
Formula: c = √(a² + b²) or c² = a² + b²
Denne formelen er basert på Pythagoras teorem som ganske enkelt kan brukes ved å ta en kvadratrot av summen av kvadrater av tilstøtende og motsatte.
2) Vinkel og ett ben
Formula: c = a / sin(α) = b / sin(β)
Du kan også beregne hypotenusen ved å bruke sinusloven, som er grunnlaget for denne formelen.
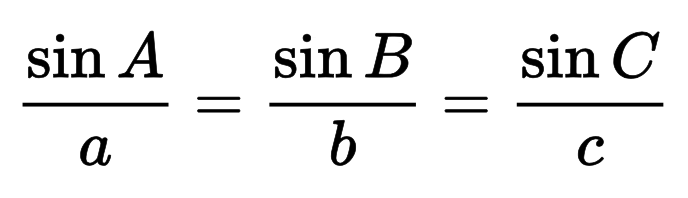
Sinusens generelle lov
3) Område og ett ben
Formula: c = √(a² + b²) = √(a² + (area _ 2 / a)²) = √((area _ 2 / b)² + b²)
Denne formelen er basert på formelen vi bruker for å beregne arealet av en trekant (a \* b / 2). Sammenlignet med de to andre ser det mer komplisert ut, men det følger samme logikk som de to andre måtene å beregne hypotenuser på.
Godt å vite om trigonometriske funksjoner
Hvis du fortsatt er opptatt av å vite mer om den rette trekanten, sjekk ut disse trigonometriske funksjonene.
Når du kjenner disse, kan du enkelt beregne sidene til den rette trekanten, eller til og med bestemme vinklene ved å bruke den trigonometriske tabellen nedenfor.
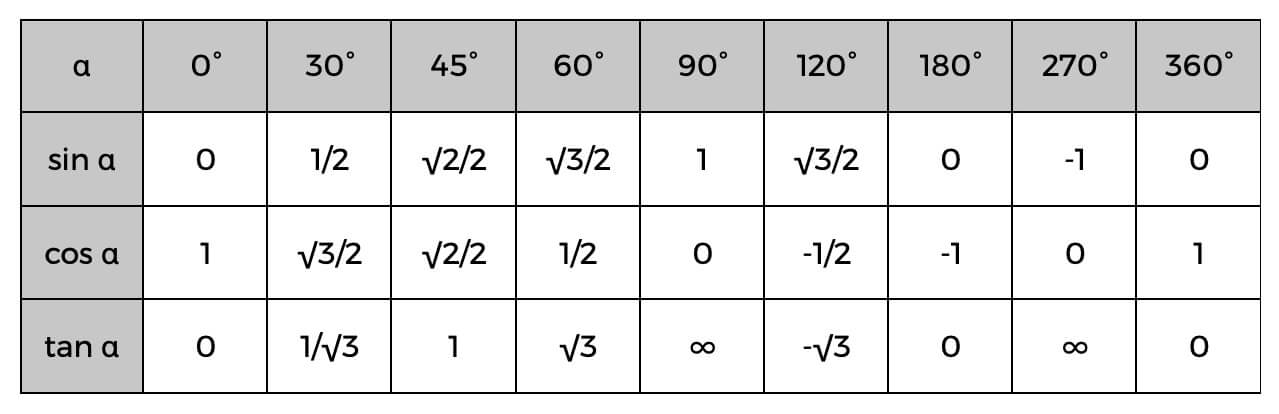
Et eksempel på dette kan være at du allerede vet verdien av hypotenusen og den tilstøtende; du kan enkelt finne cosinus til vinkelen, og sjekk deretter tabellen ovenfor for å finne den nøyaktige vinkelen eller bare et estimat av hva det kan være. Hvis cosinus til alfa (α) er 0,5, så vet vi at vinkelen er 60°.
Du kan også sjekke ut denne Wikipedia-artikkelen:
Klassifisering av trekanter basert på sidene
1) Likesidet
Denne trekanten har tre like sider. Dette resulterer i at alle vinklene er 60°.
Visuelt eksempel:

Likesidet trekant
2) Likebenet
I denne trekanten er bare to sider like.
Visuelt eksempel:

Likebent trekant
3) Skala
Ingen av sidene er like i denne trekanten.
Visuelt eksempel

Skala trekant
Klassifisering av trekanter basert på vinklene
1) Akutt
Alle tre vinklene i denne trekanten er mindre enn 90°.
Visuelt eksempel:

Akutt trekant
2) Rett
Denne trekanten har bare én 90° vinkel, noe som resulterer i at de to andre er mindre enn 90°.
Hvorfor?
α + β + γ = 180° & α = 90° → β + γ = 90° → β , γ < 90°
Visuelt eksempel:

Høyre trekant
3) Stump
Denne trekanten har en vinkel som er større enn 90°.
Visuelt eksempel:

Stump trekant
Morsomme fakta om trekanter
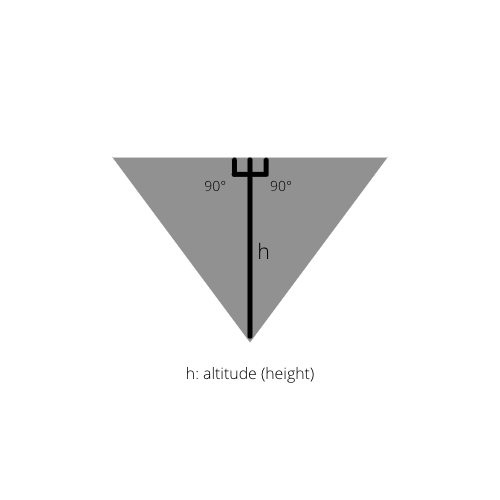
Fakta 1:
Hvis trekantens indre høyde er tegnet, får vi to rette trekanter i den opprinnelige trekanten.
Fakta 2:
Som vi vet, er arealet av en hvilken som helst trekant (A) halvparten av høyden multiplisert med grunnflaten (A = 1/2 _ b _ h). Denne formelen kan skrives på en spesiell måte for den likebenede rettvinklede trekanten siden arealet er halvparten av et kvadrats areal.
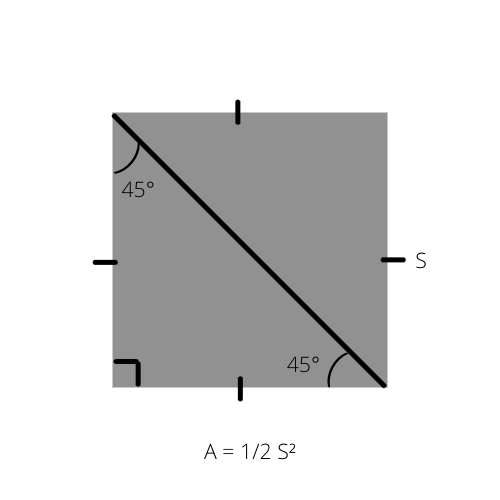
A er arealet av trekanten, og S siden av kvadratet.
Fakta 3:
Summen av alle tre vinklene i en trekant er alltid 180°. Dette gjelder alle trekanter.
Artikkelforfatter
Parmis Kazemi
Parmis er en innholdsskaper som har en lidenskap for å skrive og skape nye ting. Hun er også sterkt interessert i teknologi og liker å lære nye ting.
Trekanthypotenuskalkulator Norsk
Publisert: Wed Oct 27 2021
I kategori Matematiske kalkulatorer
Legg til Trekanthypotenuskalkulator på ditt eget nettsted