Matematiska Räknare
Triangel Hypotenusa Räknare
Ta reda på hypotenusa för alla typer av trianglar enkelt med vår gratis matematikkalkylator!
Triangel hypotenusa med två sidor
Triangel hypotenusa vid en sida och area
Innehållsförteckning
Vad är hypotenusan i en triangel?
Hypotenusan är den längsta sidan av en triangel. Det är också den sida som är motsatt från rät vinkel (90°).
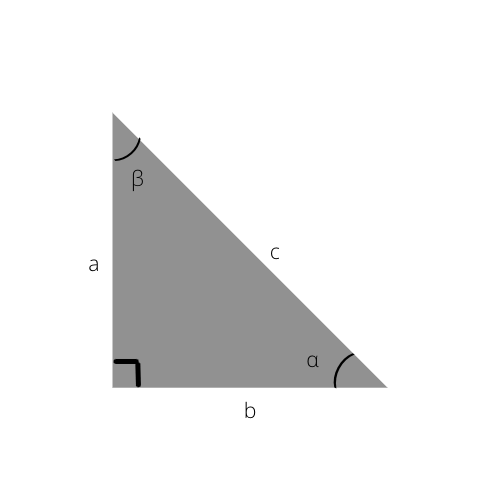
Hypotenusan är c i denna triangel.
Du kan också kolla in denna Wikipedia-artikel:
Varför är hypotenusan den längsta sidan av triangeln?
Efter att ha observerat bilden ovan, och andra räta trianglar, kommer du att märka att hypotenusan alltid är den längsta sidan av alla räta trianglar. Detta beror helt enkelt på att den är placerad mitt emot den största vinkeln, 90°-vinkeln.
detta kan också bevisas matematiskt genom att använda Pythagoras sats:
a² + b² = c²
a² > b² , a² > c²
a > b , a > c
Som du ser är resultatet av operationen ovan att "a" (hypotenusan) är större än de andra två sidorna.
Hur beräknar man hypotenusan i en triangel?
Detta kan göras på 3 olika sätt, beroende på den givna informationen som kan vara en variation av faktorerna nedan:
a: motsatt sida
b: intilliggande sida
c: hypotenussidan
α: vinkel mellan intilliggande och hypotenusa
β: vinkel mellan motsatt och hypotenusa
1) Två rätvinkliga triangelben
Formula: c = √(a² + b²) or c² = a² + b²
Denna formel är baserad på Pythagoras sats som helt enkelt kan användas genom att ta kvadratroten av summan av kvadraterna av intilliggande och motsatta.
2) Vinkel och ett ben
Formula: c = a / sin(α) = b / sin(β)
Du kan också beräkna hypotenusan genom att använda sinuslagen, som är grunden för denna formel.
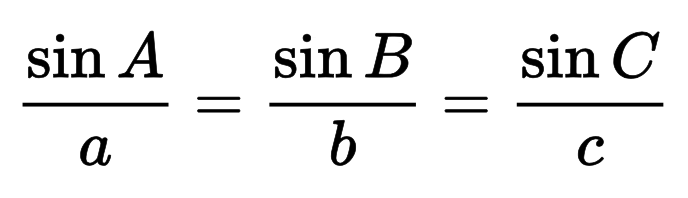
Sinusens allmänna lag
3) Område och ett ben
Formula: c = √(a² + b²) = √(a² + (area _ 2 / a)²) = √((area _ 2 / b)² + b²)
Denna formel är baserad på formeln vi använder för att beräkna arean av en triangel (a \* b / 2). Jämfört med de andra två ser det mer komplicerat ut, men det följer samma logik som de andra två sätten att beräkna hypotenusor.
Bra att veta om trigonometriska funktioner
Om du fortfarande är sugen på att veta mer om den högra triangeln, kolla in dessa trigonometriska funktioner.
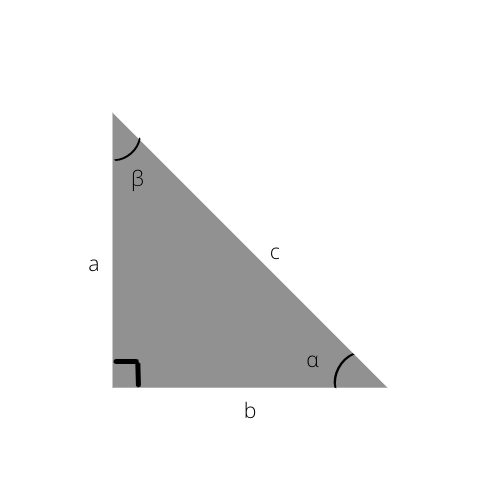
Genom att känna till dessa kan du enkelt beräkna sidorna av den räta triangeln, eller till och med bestämma vinklarna med hjälp av den trigonometriska tabellen nedan.
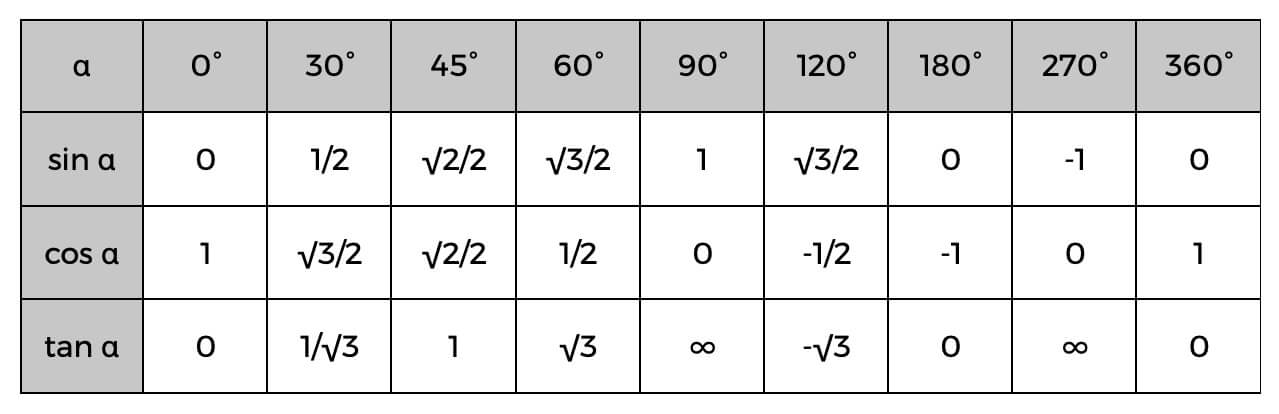
Ett exempel på detta kan vara att du redan vet värdet på hypotenusan och den intilliggande; du kan enkelt hitta cosinus för vinkeln, kolla sedan tabellen ovan för att hitta den exakta vinkeln eller bara en uppskattning av vad det kan vara. Om cosinus för alfa (α) är 0,5 så vet vi att vinkeln är 60°.
Du kan också kolla in denna Wikipedia-artikel:
Klassificering av trianglar baserat på sidorna
1) Liksidig
Denna triangel har tre lika sidor. Detta resulterar i att alla vinklar är 60°.
Visuellt exempel:

Liksidig triangel
2) Likbent
I denna triangel är bara två sidor lika.
Visuellt exempel:

Likbent triangel
3) Skala
Ingen av sidorna är lika i denna triangel.
Visuellt exempel

Skalen triangel
Klassificering av trianglar utifrån vinklarna
1) Akut
Alla tre vinklarna i denna triangel är mindre än 90°.
Visuellt exempel:

Akut triangel
2) Rätt
Denna triangel har bara en 90° vinkel, vilket resulterar i att de andra två är mindre än 90°.
Varför?
α + β + γ = 180° & α = 90° → β + γ = 90° → β , γ < 90°
Visuellt exempel:

Rätt triangel
3) Trubbig
Denna triangel har en vinkel som är större än 90°.
Visuellt exempel:

Trubbig triangel
Roliga fakta om trianglar
Fakta 1:
Om triangelns inre höjd är ritad får vi två räta trianglar i den ursprungliga triangeln.
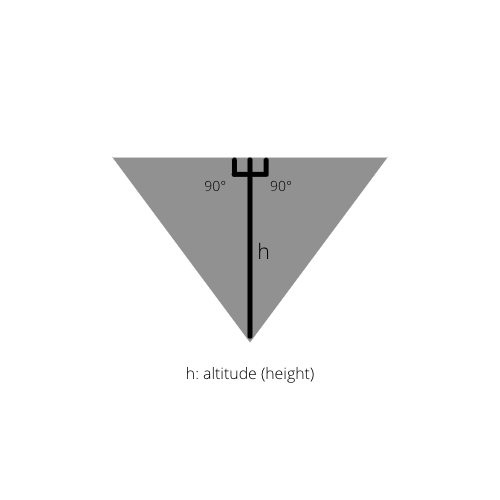
Fakta 2:
Som vi vet är arean av en triangel (A) hälften av höjden multiplicerad med basen (A = 1/2 _ b _ h). Denna formel kan skrivas på ett speciellt sätt för den likbenta rätvinkliga triangeln eftersom dess area är hälften av en kvadrats area.
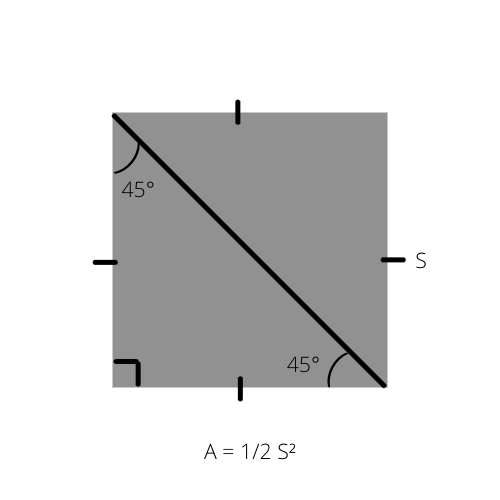
A är triangelns area och S sidan av kvadraten.
Fakta 3:
Summan av alla tre vinklarna i en triangel är alltid 180°. Detta gäller alla trianglar.
Artikelförfattare
Parmis Kazemi
Parmis är en innehållsskapare som har en passion för att skriva och skapa nya saker. Hon är också mycket intresserad av teknik och tycker om att lära sig nya saker.
Triangel Hypotenusa Räknare Svenska
Publicerad: Wed Oct 27 2021
I kategori Matematiska räknare
Lägg till Triangel Hypotenusa Räknare på din egen webbplats