Matematiksel Hesap Makineleri
Üçgen Hipotenüs Hesaplayıcı
Ücretsiz matematik hesaplayıcımızla her tür üçgen için hipotenüsü kolayca bulun!
İki kenarlı üçgen hipotenüs
Bir kenar ve alan ile üçgen hipotenüs
İçindekiler
Bir üçgenin hipotenüsü nedir?
Hipotenüs, bir üçgenin en uzun kenarıdır. Aynı zamanda dik açının (90°) karşı tarafıdır.
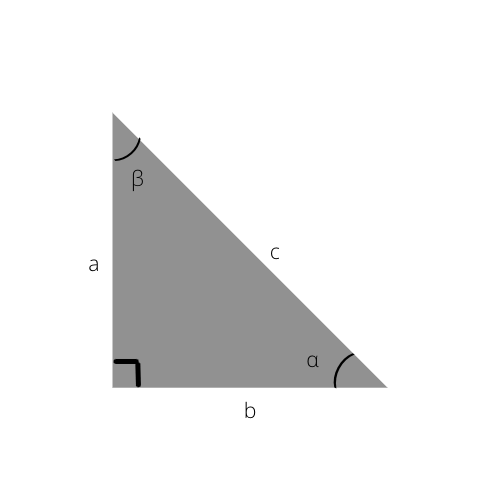
Bu üçgende hipotenüs c'dir.
Bu Wikipedia makalesine de göz atabilirsiniz:
Hipotenüs neden üçgenin en uzun kenarıdır?
Yukarıdaki resmi ve diğer dik üçgenleri inceledikten sonra, hipotenüsün her zaman tüm dik üçgenlerin en uzun kenarı olduğunu fark edeceksiniz. Bunun nedeni, en büyük açı olan 90° açının karşısında yer almasıdır.
bu Pisagor Teoremi kullanılarak matematiksel olarak da kanıtlanabilir:
a² + b² = c²
a² > b² , a² > c²
a > b , a > c
Gördüğünüz gibi, yukarıdaki işlemin sonucu "a"nın (hipotenüs) diğer iki kenardan daha büyük olmasıdır.
Bir üçgenin hipotenüsü nasıl hesaplanır?
Bu, aşağıda listelenen faktörlerin bir varyasyonu olabilecek verilen bilgilere bağlı olarak 3 farklı şekilde yapılabilir:
a: karşı taraf
b: bitişik taraf
c: hipotenüs tarafı
α: komşu ve hipotenüs arasındaki açı
β: zıt ve hipotenüs arasındaki açı
1) İki dik üçgen bacak
Formula: c = √(a² + b²) or c² = a² + b²
Bu formül, komşu ve zıt karelerin toplamının karekökünü alarak basitçe kullanılabilen Pisagor teoremine dayanmaktadır.
2) Açı ve tek bacak
Formula: c = a / sin(α) = b / sin(β)
Bu formülün temeli olan sinüs yasasını kullanarak hipotenüsü de hesaplayabilirsiniz.
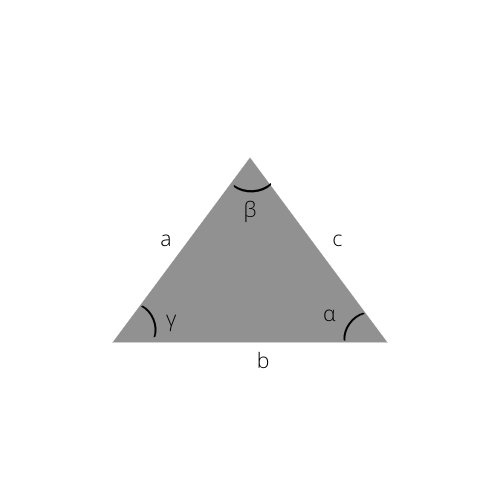
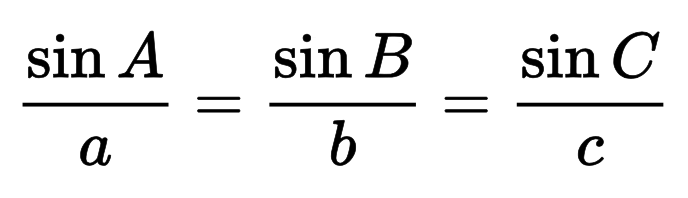
Sinüslerin genel yasası
3) Alan ve tek bacak
Formula: c = √(a² + b²) = √(a² + (area _ 2 / a)²) = √((area _ 2 / b)² + b²)
Bu formül, bir üçgenin (a \* b / 2) alanını hesaplamak için kullandığımız formüle dayanmaktadır. Diğer ikisine kıyasla daha karmaşık görünüyor, ancak diğer iki hipotenüs hesaplama yöntemiyle aynı mantığı izliyor.
Trigonometrik fonksiyonlar hakkında bilinmesi gerekenler
Hala dik üçgen hakkında daha fazla bilgi edinmek istiyorsanız, bu Trigonometrik fonksiyonlara göz atın.
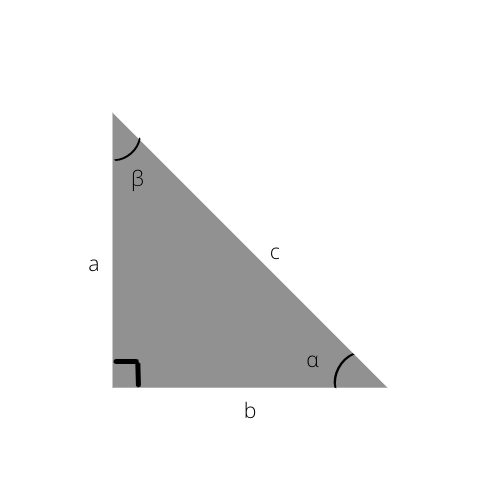
Bunları bilerek, aşağıdaki Trigonometrik tabloyu kullanarak dik üçgenin kenarlarını kolayca hesaplayabilir, hatta açıları belirleyebilirsiniz.
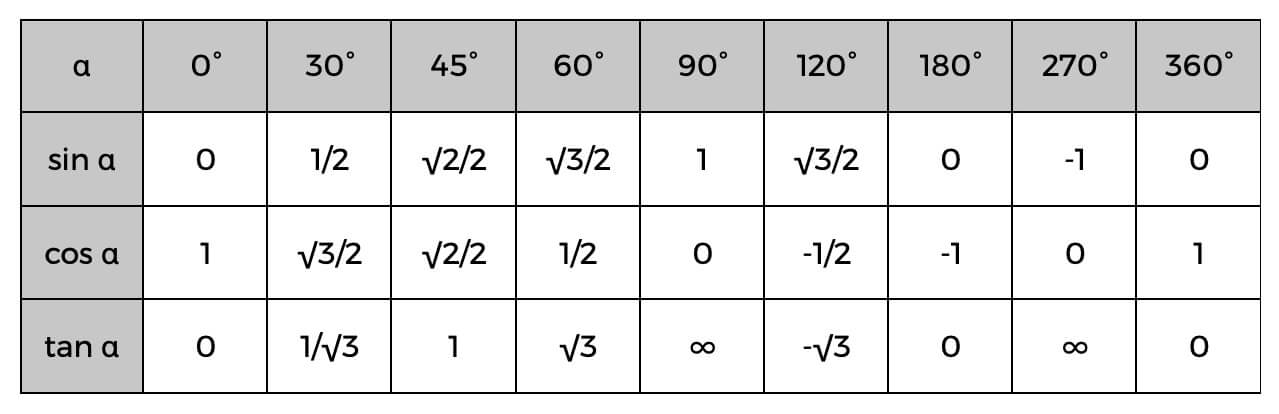
Bunun bir örneği, hipotenüsün ve komşunun değerini zaten biliyor olmanız olabilir; açının kosinüsünü kolayca bulabilir, ardından tam açıyı veya ne olabileceğine dair bir tahmin bulmak için yukarıdaki tabloyu kontrol edebilirsiniz. Alfa (α)'nın kosinüsü 0,5 ise, açının 60° olduğunu biliyoruz.
Bu Wikipedia makalesine de göz atabilirsiniz:
Kenarlara göre üçgenlerin sınıflandırılması
1) eşkenar
Bu üçgenin üç eşit kenarı vardır. Bu, tüm açıların 60° olmasıyla sonuçlanır.
Görsel örnek:

Eşkenar üçgen
2) ikizkenar
Bu üçgende sadece iki kenar birbirine eşittir.
Görsel örnek:

İkizkenar üçgen
3) skalen
Bu üçgende hiçbir kenar eşit değildir.
Görsel örnek

Eşkenar olmayan üçgen
Açılarına göre üçgenlerin sınıflandırılması
1) akut
Bu üçgendeki üç açı da 90°'den küçüktür.
Görsel örnek:

Dar üçgen
2) Sağ
Bu üçgenin yalnızca bir 90° açısı vardır, bu da diğer ikisinin 90°'den küçük olmasına neden olur.
Niye ya?
α + β + γ = 180° & α = 90° → β + γ = 90° → β , γ < 90°
Görsel örnek:

sağ üçgen
3) geniş
Bu üçgenin bir açısı 90°'den büyük.
Görsel örnek:

Geniş açılı üçgen
Üçgenler hakkında eğlenceli gerçekler
Gerçek 1:
Üçgenin iç yüksekliği çizilirse, orijinal üçgende iki dik üçgen elde ederiz.
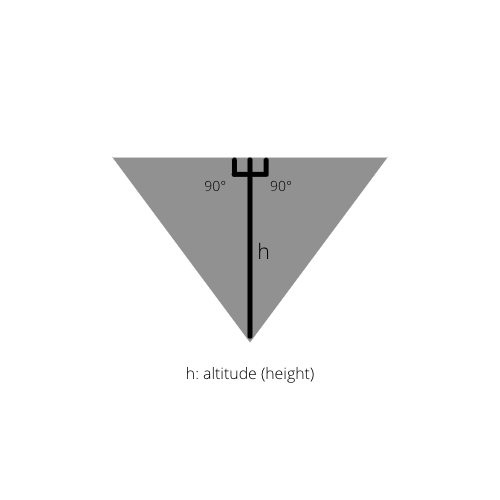
Gerçek 2:
Bildiğimiz gibi, herhangi bir üçgenin (A) alanı, yüksekliğin tabanla çarpımının yarısıdır (A = 1/2 _ b _ h). Bu formül, alanı bir karenin alanının yarısı olduğu için ikizkenar dik üçgen için özel bir şekilde yazılabilir.
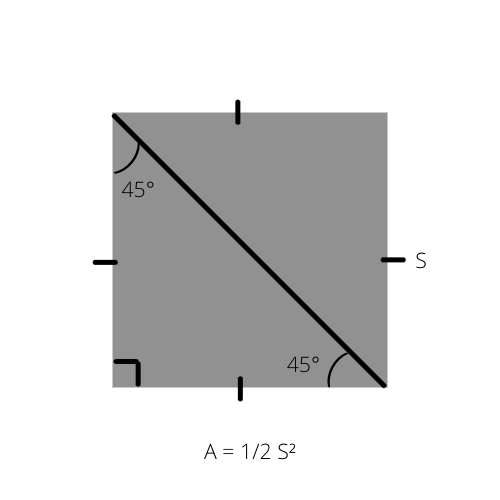
A üçgenin alanı ve S karenin kenarıdır.
Gerçek 3:
Bir üçgenin üç açısının toplamı her zaman 180°'dir. Bu tüm üçgenler için geçerlidir.
makale yazarı
Parmis Kazemi
Parmis, yeni şeyler yazma ve yaratma tutkusu olan bir içerik yaratıcısıdır. Ayrıca teknoloji ile yakından ilgileniyor ve yeni şeyler öğrenmekten hoşlanıyor.
Üçgen Hipotenüs Hesaplayıcı Türkçe
Yayınlanan: Wed Oct 27 2021
Matematiksel hesap makineleri kategorisinde
Üçgen Hipotenüs Hesaplayıcı kendi web sitenize ekleyin
Üçgen Hipotenüs Hesaplayıcı diğer dillerde
Kalkulator Hipotenusa SegitigaCalculator De Ipotenuză TriunghiКалькулятар Гіпатэнузы ТрохкутнікаKalkulačka Prepony TrojuholníkaКалкулатор За Хипотенуза На ТриъгълникKalkulator Hipotenuze TrokutaTrikampio Hipotenuzės SkaičiuotuvasCalcolatrice Triangolo IpotenusaTriangle Hypotenuse CalculatorKalkulator Hipotenus Segitiga