Kalkulator Matematik
Kalkulator Hipotenus Segitiga
Ketahui hipotenus untuk semua jenis segi tiga dengan mudah dengan kalkulator matematik percuma kami!
Segi tiga hipotenus dengan dua sisi
Segi tiga hipotenus dengan satu sisi dan luas
Isi kandungan
Apakah hipotenus bagi segi tiga?
Hiptenus ialah sisi terpanjang bagi segitiga. Ia juga adalah sisi bertentangan dari sudut kanan (90°).
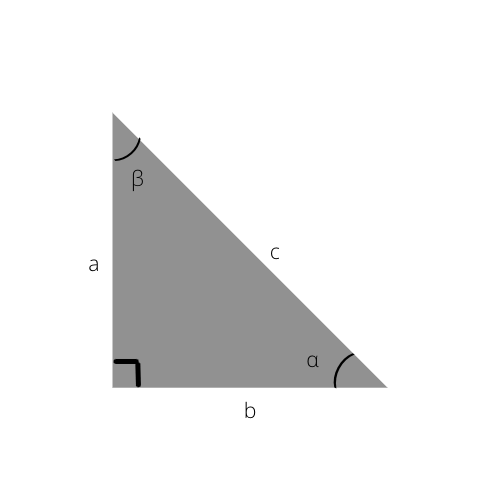
Hipotenus ialah c dalam segi tiga ini.
Anda juga boleh menyemak artikel Wikipedia ini:
Mengapakah hipotenus adalah sisi terpanjang bagi segi tiga?
Selepas memerhatikan gambar di atas, dan segi tiga tegak yang lain, anda akan dapati bahawa hipotenus sentiasa merupakan sisi terpanjang bagi semua segi tiga tegak. Ini semata-mata kerana ia terletak bertentangan dengan sudut terbesar, sudut 90°.
ini juga boleh dibuktikan secara matematik dengan menggunakan Teorem Pythagoras:
a² + b² = c²
a² > b² , a² > c²
a > b , a > c
Seperti yang anda lihat, hasil daripada operasi di atas ialah "a" (hipotenus) adalah lebih besar daripada dua sisi yang lain.
Bagaimana untuk mengira hipotenus segitiga?
Ini boleh dilakukan dalam 3 cara berbeza, bergantung pada maklumat yang diberikan yang boleh menjadi variasi faktor yang disenaraikan di bawah:
a: bertentangan
b: sebelah bersebelahan
c: sisi hipotenus
α: sudut antara bersebelahan dan hipotenus
β: sudut antara bertentangan dan hipotenus
1) Dua kaki segi tiga tepat
Formula: c = √(a² + b²) or c² = a² + b²
Formula ini berdasarkan teorem Pythagoras yang boleh digunakan secara ringkas dengan mengambil punca kuasa dua hasil tambah kuasa dua bersebelahan dan bertentangan.
2) Sudut dan satu kaki
Formula: c = a / sin(α) = b / sin(β)
Anda juga boleh mengira hipotenus dengan menggunakan hukum sinus, yang merupakan asas formula ini.
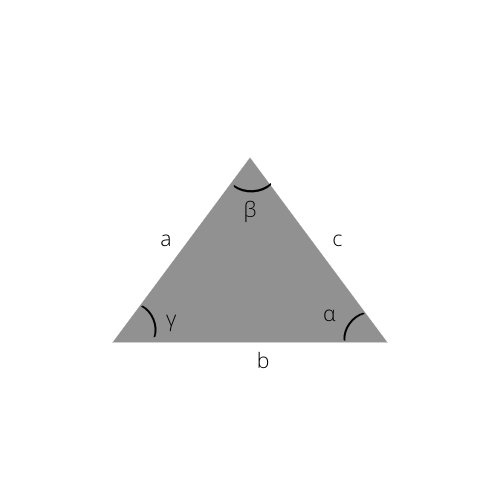
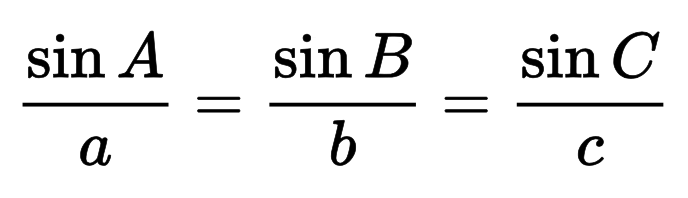
Hukum am sinus
3) Kawasan dan sebelah kaki
Formula: c = √(a² + b²) = √(a² + (area _ 2 / a)²) = √((area _ 2 / b)² + b²)
Formula ini adalah berdasarkan formula yang kami gunakan untuk mengira luas segi tiga (a \* b / 2). Berbanding dengan dua yang lain ia kelihatan lebih rumit, bagaimanapun, ia mengikut logik yang sama seperti dua cara lain untuk mengira hipotenus.
Baik untuk mengetahui tentang fungsi Trigonometri
Jika anda masih berminat untuk mengetahui lebih lanjut tentang segi tiga tepat, lihat fungsi Trigonometri ini.
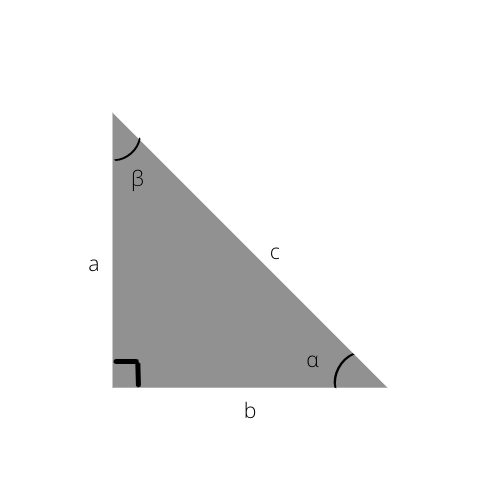
Mengetahui ini, anda boleh mengira sisi segi tiga tepat dengan mudah, atau bahkan menentukan sudut menggunakan jadual Trigonometri di bawah.
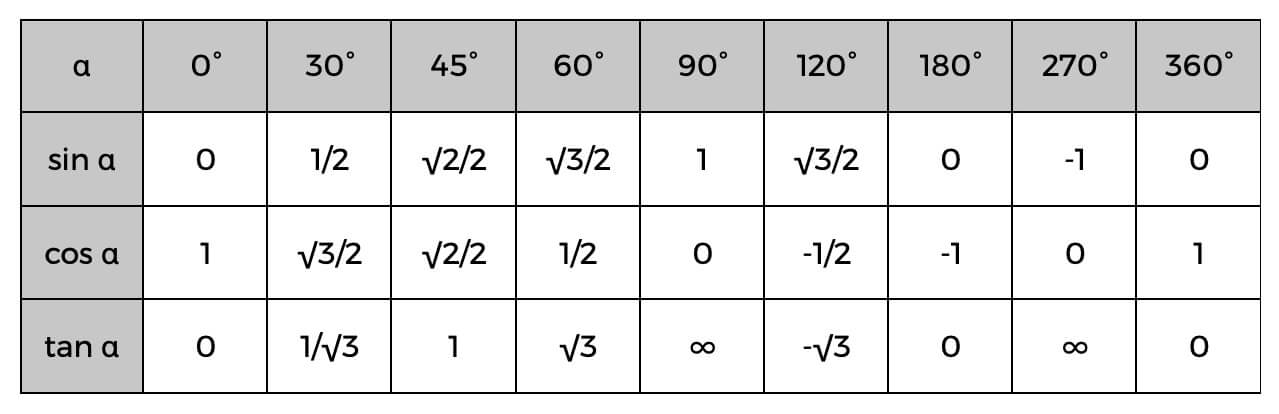
Contohnya ialah anda sudah mengetahui nilai hipotenus dan yang bersebelahan; anda boleh mencari kosinus sudut dengan mudah, kemudian semak jadual di atas untuk mencari sudut yang tepat atau hanya anggaran perkara itu. Jika kosinus alfa (α) ialah 0.5, maka kita tahu bahawa sudutnya ialah 60°.
Anda juga boleh menyemak artikel Wikipedia ini:
Pengelasan segi tiga berdasarkan sisi
1) Sama sisi
Segitiga ini mempunyai tiga sisi yang sama. Ini menyebabkan semua sudut adalah 60°.
Contoh visual:

segi tiga sama sisi
2) Sama kaki
Dalam segi tiga ini hanya dua sisi yang sama.
Contoh visual:

Segitiga sama kaki
3) Skala
Tiada satu pun sisi yang sama dalam segi tiga ini.
Contoh visual

Segitiga skala
Pengelasan segitiga berdasarkan sudut
1) Akut
Ketiga-tiga sudut dalam segi tiga ini adalah lebih kecil daripada 90°.
Contoh visual:

Segitiga akut
2) Betul
Segitiga ini hanya mempunyai satu sudut 90°, menyebabkan dua yang lain kurang daripada 90°.
kenapa?
α + β + γ = 180° & α = 90° → β + γ = 90° → β , γ < 90°
Contoh visual:

Segitiga kanan
3) Bodoh
Segitiga ini mempunyai satu sudut yang lebih besar daripada 90°.
Contoh visual:

Segi tiga tumpul
Fakta menarik tentang segitiga
Fakta 1:
Jika altitud dalam segitiga itu dilukis, kita mendapat dua segi tiga tepat dalam segi tiga asal.
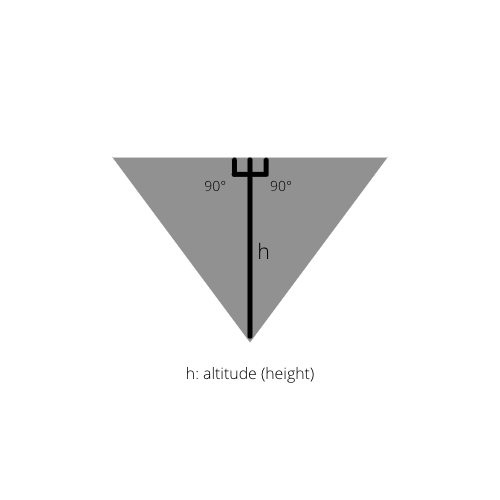
Fakta 2:
Seperti yang kita ketahui, luas mana-mana segitiga (A) ialah separuh daripada ketinggian didarab dengan tapak (A = 1/2 _ b _ h). Formula ini boleh ditulis dengan cara khas untuk segi tiga sama kaki kerana luasnya ialah separuh daripada luas segi empat sama.
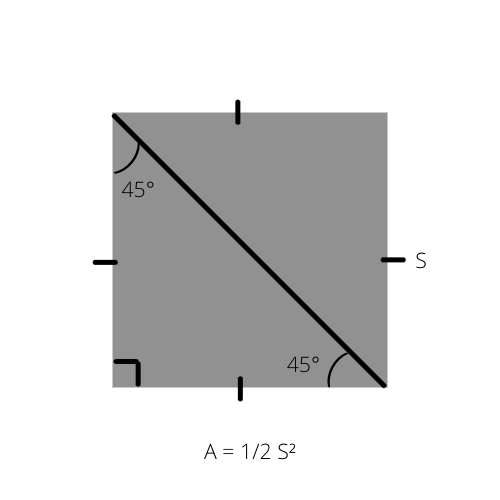
A ialah luas segi tiga, dan S sisi segi empat sama.
Fakta 3:
Jumlah ketiga-tiga sudut segitiga adalah sentiasa 180°. Ini benar tentang semua segi tiga.
Pengarang artikel
Parmis Kazemi
Parmis adalah pencipta kandungan yang mempunyai minat untuk menulis dan mencipta perkara baru. Dia juga sangat berminat dengan teknologi dan suka belajar perkara baru.
Kalkulator Hipotenus Segitiga Bahasa Melayu
Diterbitkan: Wed Oct 27 2021
Dalam kategori Kalkulator matematik
Tambahkan Kalkulator Hipotenus Segitiga ke laman web anda sendiri