Riyazi Hesablayıcılar
Üçbucaqlı Hipotenuz Kalkulyatoru
Pulsuz riyaziyyat kalkulyatorumuzla hər cür üçbucaqlar üçün hipotenuzanı asanlıqla tapın!
Üçbucağın iki tərəfi hipotenuzası
Bir tərəfi və sahəsi olan üçbucaq hipotenuzası
Mündəricat
Üçbucağın hipotenuzası nədir?
Hipotenuza üçbucağın ən uzun tərəfidir. O, həm də düzgün bucaqdan (90°) əks tərəfdir.
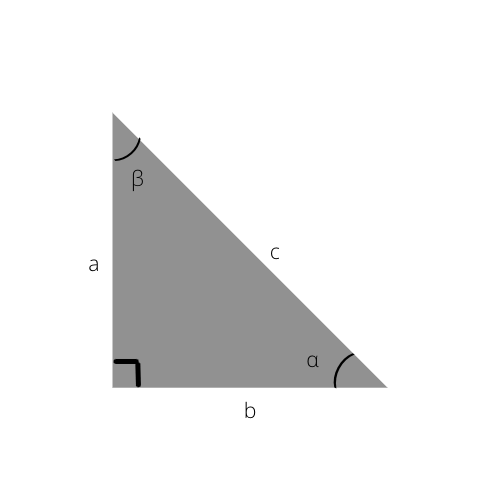
Bu üçbucaqda hipotenuz c-dir.
Bu Vikipediya məqaləsinə də baxa bilərsiniz:
Niyə hipotenuza üçbucağın ən uzun tərəfidir?
Yuxarıdakı şəkli və digər düzbucaqlıları müşahidə etdikdən sonra görəcəksiniz ki, hipotenuz həmişə bütün düzbucaqlıların ən uzun tərəfidir. Bu, sadəcə olaraq, ən böyük bucağın, 90° bucağın əksinə yerləşdiyinə görədir.
Bunu Pifaqor teoremindən istifadə etməklə də riyazi olaraq sübut etmək olar:
a² + b² = c²
a² > b² , a² > c²
a > b , a > c
Gördüyünüz kimi, yuxarıdakı əməliyyatın nəticəsi "a"nın (hipotenuzanın) digər iki tərəfdən daha böyük olmasıdır.
Üçbucağın hipotenuzunu necə hesablamaq olar?
Bu, aşağıda sadalanan amillərin variasiyası ola biləcək verilən məlumatdan asılı olaraq 3 fərqli şəkildə edilə bilər:
a: qarşı tərəf
b: bitişik tərəf
c: hipotenuz tərəfi
α: bitişik və hipotenuz arasındakı bucaq
β: əks və hipotenuz arasındakı bucaq
1) İki düzbucaqlı üçbucaqlı ayaq
Formula: c = √(a² + b²) or c² = a² + b²
Bu düstur Pifaqor teoreminə əsaslanır, ondan sadəcə qonşu və əks tərəflərin kvadratlarının cəminin kvadrat kökünü götürməklə istifadə etmək olar.
2) Bucaq və bir ayaq
Formula: c = a / sin(α) = b / sin(β)
Bu düsturun əsasını təşkil edən sinus qanunundan istifadə edərək hipotenuzanı da hesablaya bilərsiniz.
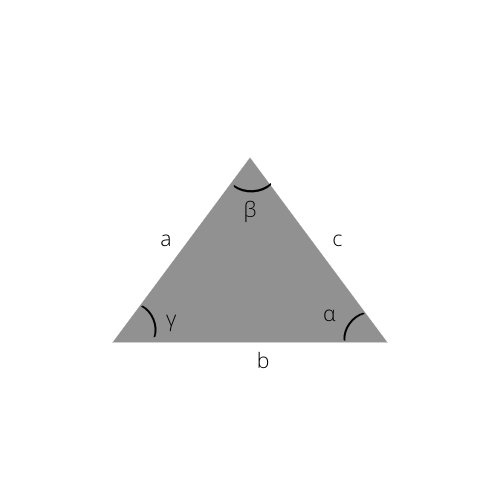
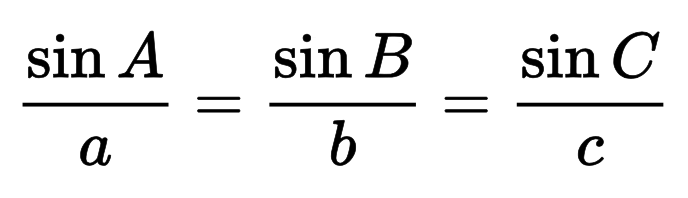
Sinusların ümumi qanunu
3) Sahə və bir ayaq
Formula: c = √(a² + b²) = √(a² + (area _ 2 / a)²) = √((area _ 2 / b)² + b²)
Bu düstur üçbucağın (a \* b / 2) sahəsini hesablamaq üçün istifadə etdiyimiz düstura əsaslanır. Digər ikisi ilə müqayisədə bu, daha mürəkkəb görünür, lakin hipotenusların hesablanmasının digər iki yolu ilə eyni məntiqə uyğundur.
Triqonometrik funksiyalar haqqında bilmək yaxşıdır
Əgər hələ də düz üçbucaq haqqında daha çox bilmək istəyirsinizsə, bu Triqonometrik funksiyaları yoxlayın.
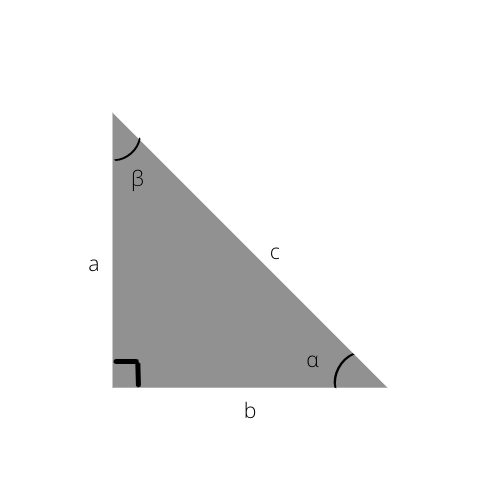
Bunları bilməklə siz sağ üçbucağın tərəflərini asanlıqla hesablaya, hətta aşağıdakı Triqonometrik cədvəldən istifadə edərək bucaqlarını təyin edə bilərsiniz.
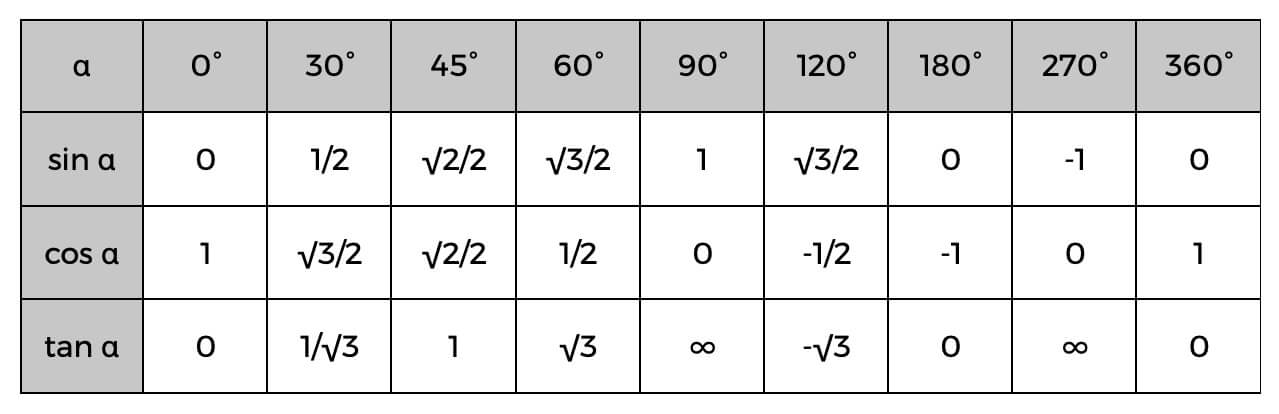
Buna misal ola bilər ki, siz artıq hipotenuzun və ona bitişik olanın dəyərini bilirsiniz; bucağın kosinusunu asanlıqla tapa bilərsiniz, sonra dəqiq bucağı tapmaq üçün yuxarıdakı cədvələ baxın və ya bunun nə ola biləcəyini təxmin edin. Əgər alfanın (α) kosinusu 0,5 olarsa, onda bucağın 60° olduğunu bilirik.
Bu Vikipediya məqaləsinə də baxa bilərsiniz:
Tərəflərə görə üçbucaqların təsnifatı
1) Bərabərtərəfli
Bu üçbucağın üç bərabər tərəfi var. Bu, bütün bucaqların 60 ° olması ilə nəticələnir.
Vizual nümunə:

Bərabər üçbucaq
2) İkitərəflilər
Bu üçbucaqda yalnız iki tərəf bərabərdir.
Vizual nümunə:

İkitərəfli üçbucaq
3) Skalen
Bu üçbucaqda tərəflərin heç biri bərabər deyil.
Vizual nümunə

Skalen üçbucağı
Bucaqlara görə üçbucaqların təsnifatı
1) Kəskin
Bu üçbucaqdakı hər üç bucaq 90°-dən kiçikdir.
Vizual nümunə:

Kəskin üçbucaq
2) sağ
Bu üçbucağın yalnız bir 90° bucağı var, nəticədə digər ikisi 90°-dən azdır.
Niyə?
α + β + γ = 180° & α = 90° → β + γ = 90° → β , γ < 90°
Vizual nümunə:

Sağ üçbucaq
3) Kütləvi
Bu üçbucağın 90°-dən böyük bir bucağı var.
Vizual nümunə:

Kəpənək üçbucaq
Üçbucaqlar haqqında maraqlı faktlar
Fakt 1:
Üçbucağın daxili hündürlüyü çəkilərsə, orijinal üçbucaqda iki düzbucaqlı alırıq.
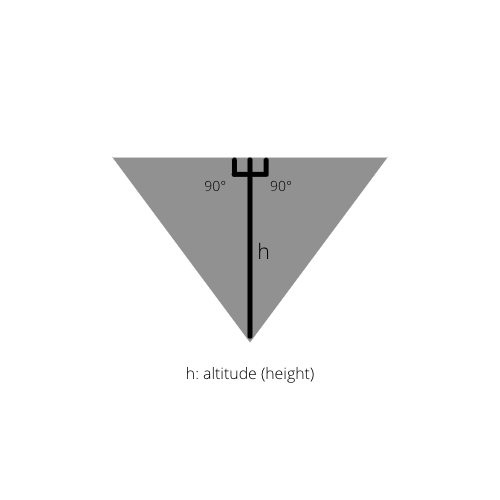
Fakt 2:
Bildiyimiz kimi, hər hansı bir üçbucağın sahəsi (A) hündürlüyün əsasla çarpılmasının yarısıdır (A = 1/2 _ b _ h). Bu düstur ikitərəfli düzbucaqlı üçün xüsusi şəkildə yazıla bilər, çünki onun sahəsi kvadratın sahəsinin yarısıdır.
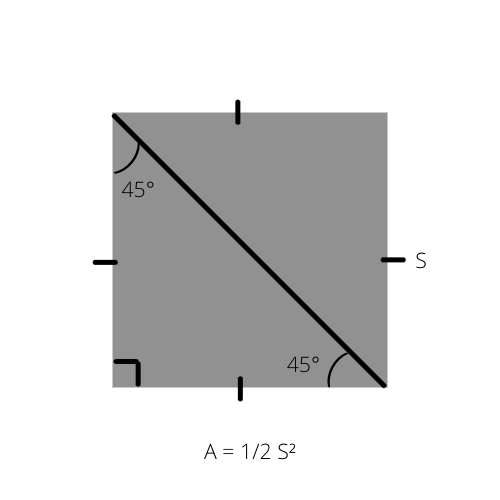
A üçbucağın sahəsi, S isə kvadratın tərəfidir.
Fakt 3:
Üçbucağın hər üç bucağının cəmi həmişə 180°-dir. Bu, bütün üçbucaqlara aiddir.
Məqalə müəllifi
Parmis Kazemi
Parmis, yeni şeylər yazmaq və yaratmaq həvəsi olan bir məzmun yaradıcısıdır. Texnika ilə də çox maraqlanır və yeni şeylər öyrənməyi sevir.
Üçbucaqlı Hipotenuz Kalkulyatoru Azərbaycan
Yayımlandı: Wed Oct 27 2021
Riyazi hesablayıcılar kateqoriyasında
Öz saytınıza Üçbucaqlı Hipotenuz Kalkulyatoru əlavə edin