Matematiska Räknare
Kalkylator För Trigonometri
Beräkna enkelt trigonometriska värden Sin, Cos, Tan, Cot, Sec och Csc med vår gratis onlineräknare!
Kalkylator för trigonometri
Innehållsförteckning
Vad är trigonometri?
Trigonometri är en gren av matematiken som handlar om sidorna och vinklarna i en triangel. Detta ämne täcker också relevanta funktioner som används för beräkning av vinklar.
Vilka är de primära eller grundläggande trigonometriska funktionerna?
Nedan ser du en lista över de primära trigonometriska funktionerna som huvudsakligen används vid användning av trigonometri.
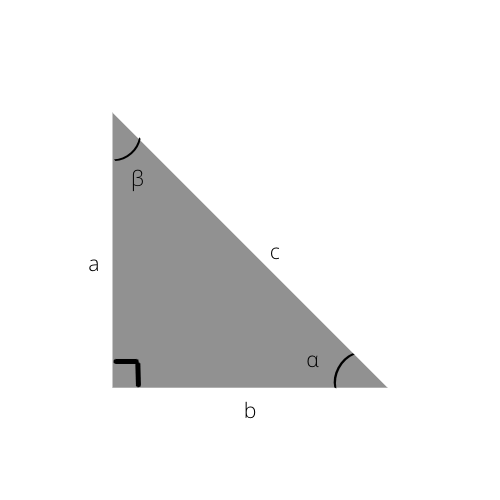
Ett exempel på en rätvinklig triangel. "α"-vinkeln i denna bild refereras till i följande formler.
1) Sinus i en vinkel
Formel: sin α = motsatt / hypotenusa
Förhållandet mellan sinus för en vinkel, i en rätvinklig triangel, är längden på motsatsen dividerat med längden på hypotenusan.
2) Cosinus för en vinkel
Formel: cos α = intilliggande / hypotenusa
Cosinus för en vinkel, i samband med en rätvinklig triangel, beräknas genom att dividera längden av den intilliggande med längden på hypotenusan.
3) Tangent av en vinkel
Formel: tan α = sin α / cos α = motsatt / intilliggande
Tangensen för en vinkel, i en rätvinklig triangel, beräknas genom att dividera sinus med cosinus. Detta kan också ersättas genom att dividera motsatsen med intilliggande.
Tänk också på den trigonometriska tabellen när du använder dessa funktioner.
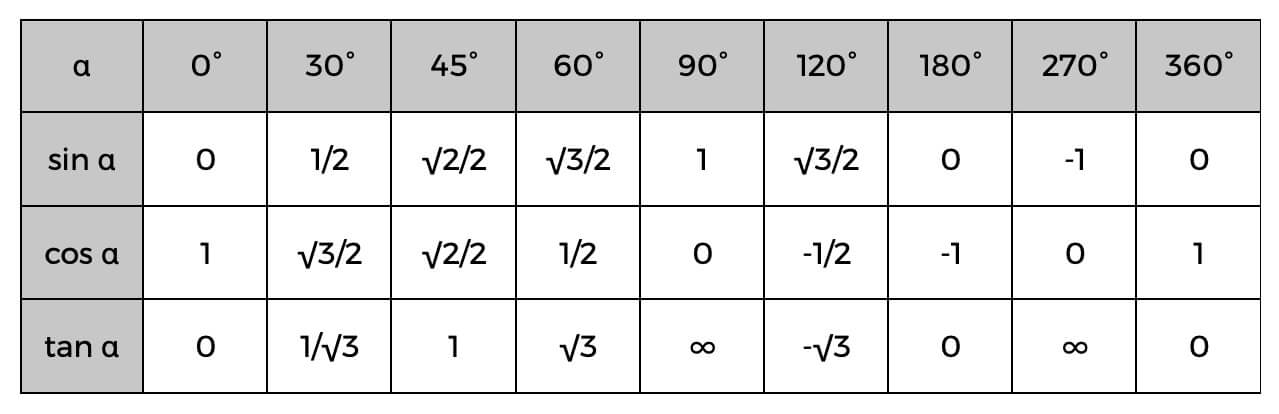
Det trigonometriska bordet
Vad är reciproka trigonometriska funktioner?
Förutom de primära trigonometriska funktionerna finns det också en annan uppsättning funktioner som inte är lika använda jämfört med den första kategorin. Dessa inkluderar secant (sec), cosecant (csc) och cotangens (cot).
Vad används trigonometri till?
Trigonometri är relaterad till trianglar, i synnerhet räta trianglar. Så var du än ser en triangel utanför matematikvärlden, slår du vad om att trigonometri är till hjälp. Ett exempel på detta är användningen av trigonometriska beräkningar inom områden som arkitektur, astronomi och kemiteknik.
Verkliga tillämpningar av trigonometri
Förutom den uppenbara användningen av trigonometri, som är i matematik, används trigonometri också i verkliga situationer och fält.
1) Arkitektur och ingenjörskonst
Det är inte så långt borta att tänka på användningen av trigonometriska funktioner i arkitektur. Dessa funktioner används mest för att beräkna längden på diagonalkopplingen som förbinder två linjer. Detta används för att beräkna den diagonala längden av ett taks lutning vid design av ett sluttande tak. Du behöver bara veta höjden och längden på taket och du är igång!

2) Astronomi
Astronomi är ett viktigt ämne som gamla kulturer mest uppmärksammade. När man talar om detta är förmodligen en av de första sakerna som kommer att tänka på konstellationerna och att beräkna deras avstånd från varandra och andra objekt i rymden, vilket är en av de enklare användningsområdena för astronomi. Med andra ord kan trigonometri användas för att beräkna solens och jordens avstånd från olika stjärnor. Stjärnornas avstånd är viktigt för att beräkna deras faktorer i astronomivärlden.
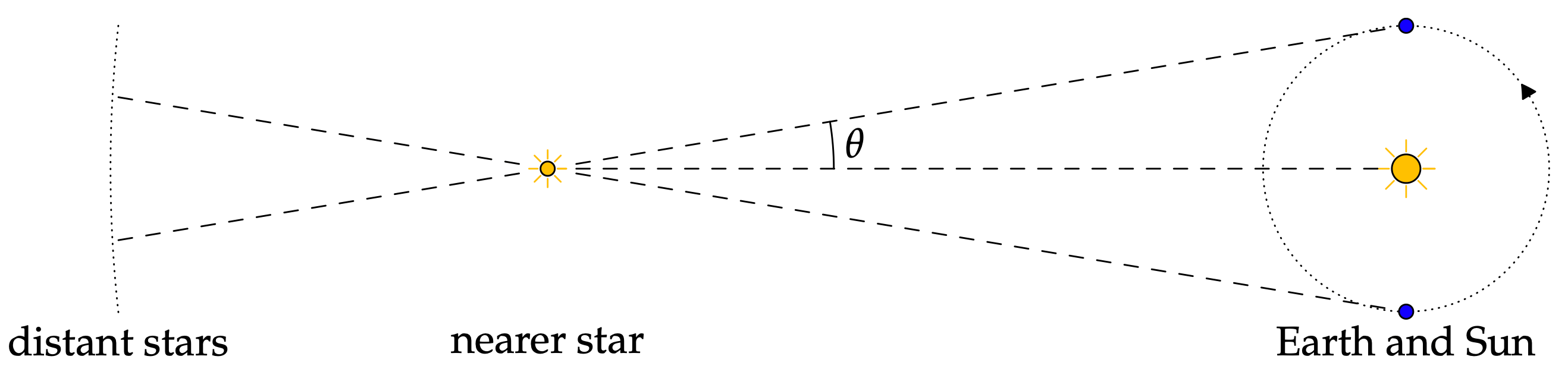
Se den här artikeln för ytterligare information om astronomi och dess relation till trigonometri:
3) Elektronik och elektroteknik
Trigonometri används för att lösa matematiska problem inom elektronik och elektroteknik, mest när man designar en modell. Ett annat exempel på vikten är när man gör estetiska tillägg och ser till att de inte stör modellens funktion.
Men trigonometriska funktioner är väldigt användbara när man arbetar med kretsar. Se det visuella exemplet nedan för ytterligare demonstration och för att få en uppfattning om hur trigonometri översätts till kretslogik.
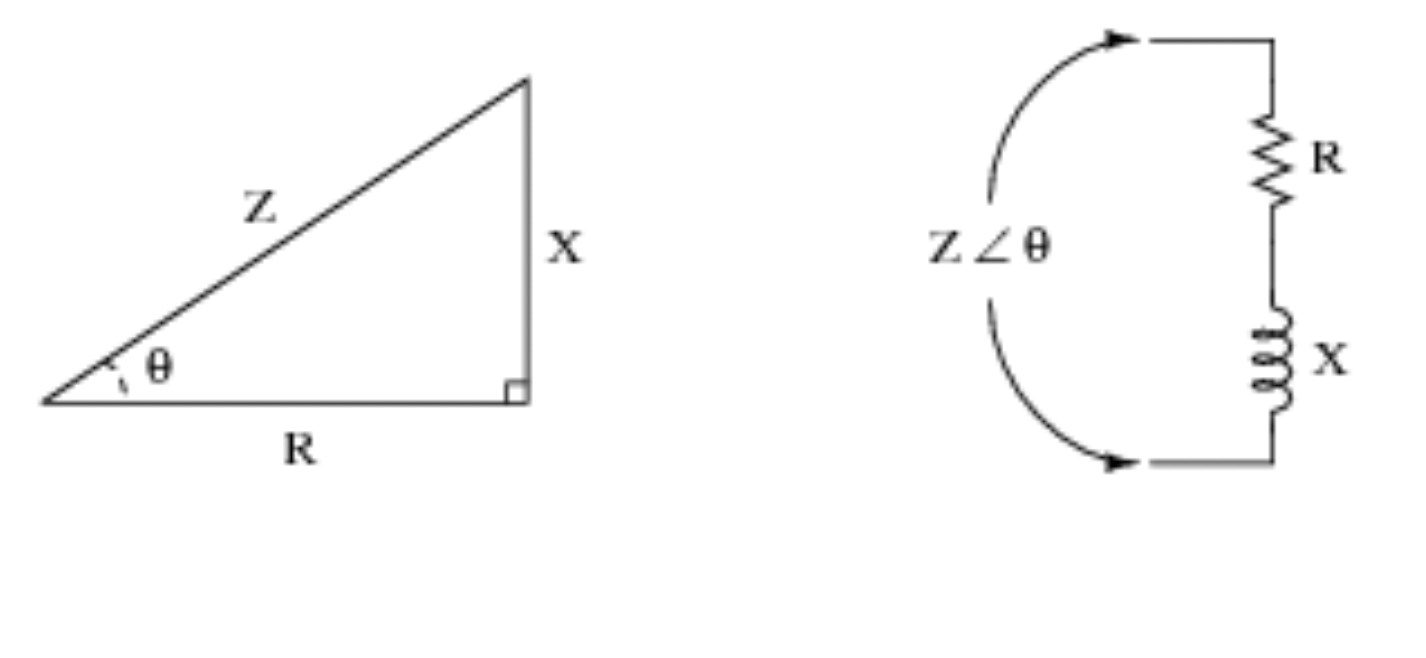
4) Seismologi
Seismologi är studiet av jordbävningar, såväl som de seismiska vågorna som rör sig genom och runt jorden. Trigonometri kommer in för att underlätta beräkningen av det vertikala och horisontella avståndet en seismisk våg färdas.

5) Lantmäteri (väg- och vattenbyggnad)
Lantmäteri har varit ett yrke som har funnits länge, åtminstone så länge som nedtecknad historia visar. Detta görs av en lantmätare som har till uppgift att noggrant mäta jordens ytor i stor skala. Du kanske har gissat användningen av trigonometri vid det här laget; i grund och botten kommer trigonometri in när besiktningsmannen behöver beräkna längden, ytorna och relativa vinklarna mellan objekten i landskapet.
Exemplet nedan är en bra visuell demonstration av vad som tidigare förklarats. En lantmätare använder trigonometriska bråktal för att beräkna sitt eget avstånd från bergstoppen eller från någon annanstans de väljer.

Artikelförfattare
Parmis Kazemi
Parmis är en innehållsskapare som har en passion för att skriva och skapa nya saker. Hon är också mycket intresserad av teknik och tycker om att lära sig nya saker.
Kalkylator För Trigonometri Svenska
Publicerad: Fri Oct 29 2021
I kategori Matematiska räknare
Lägg till Kalkylator För Trigonometri på din egen webbplats