Matematiske Regnemaskiner
Trigonometri Lommeregner
Beregn let trigonometriske værdier Sin, Cos, Tan, Cot, Sec og Csc med vores gratis online lommeregner!
Trigonometri lommeregner
Indholdsfortegnelse
Hvad er trigonometri?
Trigonometri er en gren af matematikken, der beskæftiger sig med siderne og vinklerne i en trekant. Dette emne dækker også de relevante funktioner, der bruges til beregning af vinkler.
Hvad er de primære eller grundlæggende trigonometriske funktioner?
Nedenfor vil du se en liste over de primære trigonometriske funktioner, der hovedsageligt bruges ved brug af trigonometri.
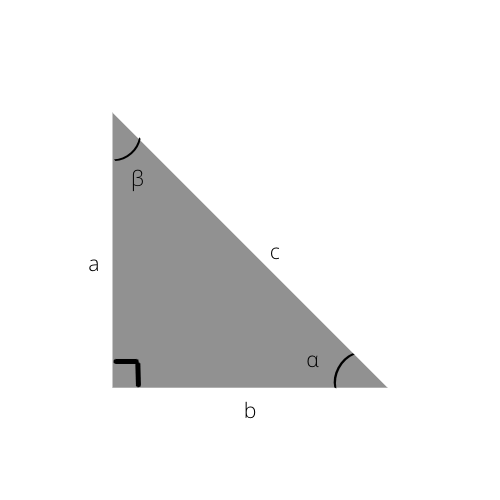
Et eksempel på en retvinklet trekant. "α"-vinklen i dette billede henvises til i følgende formler.
1) Sinus af en vinkel
Formel: sin α = modsat / hypotenusen
Forholdet mellem sinus af en vinkel, i sammenhæng med en retvinklet trekant, er længden af det modsatte divideret med længden af hypotenusen.
2) Cosinus af en vinkel
Formel: cos α = tilstødende / hypotenuse
Cosinus af en vinkel, i sammenhæng med en retvinklet trekant, beregnes ved at dividere længden af den tilstødende vinkel med længden af hypotenusen.
3) Tangent af en vinkel
Formel: tan α = sin α / cos α = modsat / tilstødende
Tangens af en vinkel, i sammenhæng med en retvinklet trekant, beregnes ved at dividere sinus med cosinus. Dette kan også erstattes ved at dividere det modsatte med det tilstødende.
Husk også den trigonometriske tabel, når du bruger disse funktioner.
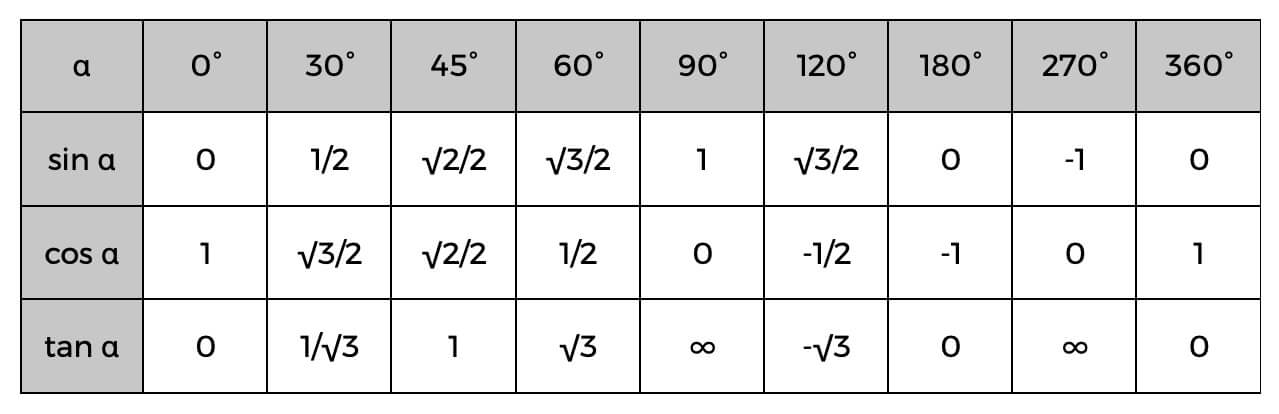
Den trigonometriske tabel
Hvad er gensidige trigonometriske funktioner?
Udover de primære trigonometriske funktioner er der også et andet sæt funktioner, der ikke er som brugt sammenlignet med den første kategori. Disse omfatter secant (sek), cosecant (csc) og cotangens (cot).
Hvad bruges trigonometri til?
Trigonometri er relateret til trekanter, især retvinklede trekanter. Så uanset hvor du ser en trekant uden for matematikverdenen, satser du på, at trigonometri er nyttig. Et eksempel på dette er brugen af trigonometriske beregninger inden for områder som arkitektur, astronomi og kemiteknik.
Virkelige anvendelser af trigonometri
Bortset fra den åbenlyse brug af trigonometri, som er i matematik, bruges trigonometri også i virkelige situationer og felter.
1) Arkitektur og teknik
Det er ikke for langt væk at tænke på brugen af trigonometriske funktioner i arkitektur. Disse funktioner bruges mest til at beregne længden af den diagonale forbindelse, der forbinder to linjer. Dette bruges til at beregne den diagonale længde af et tags hældning, når man designer et skrå tag. Du behøver kun at kende højden og længden af taget, og du er godt i gang!

2) Astronomi
Astronomi er et vigtigt emne, som gamle kulturer for det meste var opmærksomme på. Når man taler om dette, er nok en af de første ting, der kommer til at tænke på, stjernebillederne og beregningen af deres afstand fra hinanden og andre objekter i rummet, hvilket er en af de mere simple anvendelser af astronomi. Med andre ord kan trigonometri bruges til at beregne afstanden mellem solen og jorden fra forskellige stjerner. Stjernernes afstand er vigtig for at beregne deres faktorer i astronomiens verden.
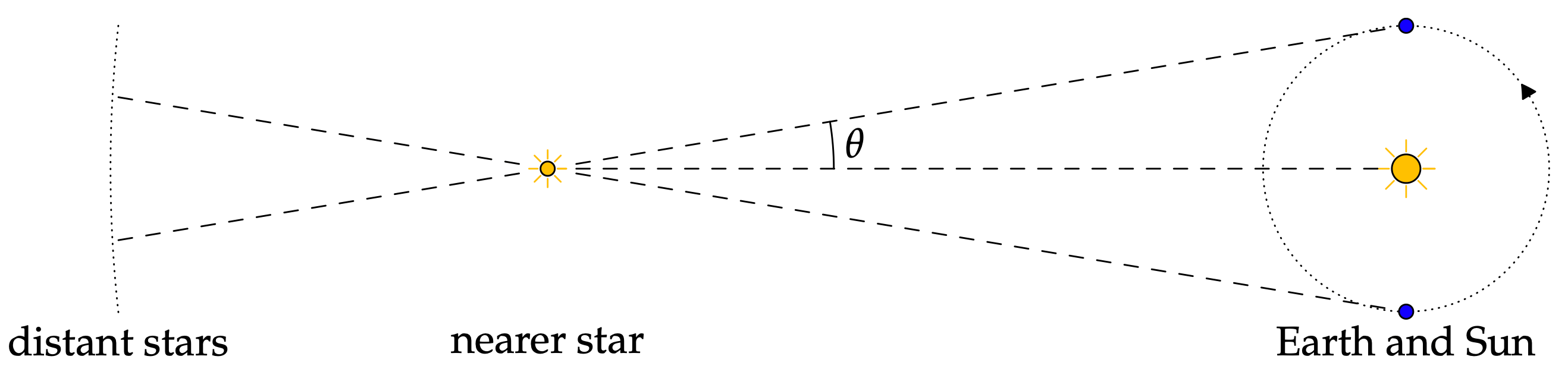
Se denne artikel for yderligere information om astronomi og dens relation til trigonometri:
3) Elektronik og elektroteknik
Trigonometri bruges til at løse matematiske problemer i elektronik og elektroteknik, mest når man designer en model. Et andet eksempel på vigtigheden er, når man laver æstetiske tilføjelser og sørger for, at de ikke forstyrrer modellens funktion.
Trigonometriske funktioner er dog meget nyttige, når du arbejder med kredsløb. Se nedenstående visuelle eksempel for yderligere demonstration og for at få en idé om, hvordan trigonometri omsættes til kredsløbslogik.
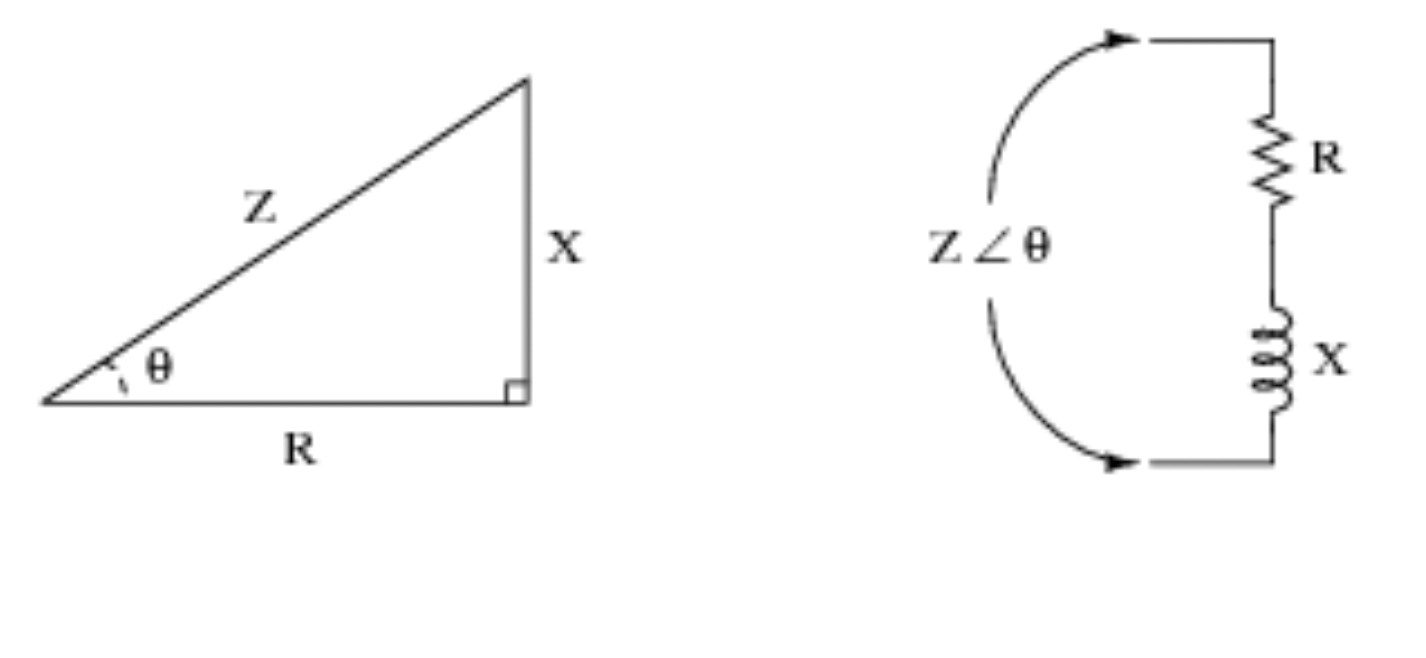
4) Seismologi
Seismologi er studiet af jordskælv, såvel som de seismiske bølger, der bevæger sig gennem og omkring jorden. Trigonometri kommer ind for at lette beregningen af den lodrette og vandrette afstand en seismisk bølge tilbagelægger.

5) Landmåling (anlægsteknik)
Landmåling har været et erhverv, der har eksisteret i lang tid, i hvert fald så længe som den registrerede historie viser. Dette gøres af en landmåler, der har til opgave at måle jordens overflader nøjagtigt i stor skala. Du har måske gættet brugen af trigonometri nu; dybest set kommer trigonometri ind, når landmåleren skal beregne længden, arealer og relative vinkler mellem objekterne i landskabet.
Eksemplet nedenfor er en god visuel demonstration af, hvad der tidligere er blevet forklaret. En landmåler bruger trigonometriske brøker til at beregne sin egen afstand fra bjergtoppen eller fra et hvilket som helst andet sted, de vælger.

Artikelforfatter
Parmis Kazemi
Parmis er en indholdsskaber, der har en passion for at skrive og skabe nye ting. Hun er også meget interesseret i teknologi og nyder at lære nye ting.
Trigonometri Lommeregner Dansk
Udgivet: Fri Oct 29 2021
I kategori Matematiske regnemaskiner
Føj Trigonometri Lommeregner til dit eget websted